Polynome, existance et unicité.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 28 Oct 2008, 19:46
par muse » 28 Oct 2008, 19:46
Bonsoir
soit le produit scalaire:
Q(t)w(t)dt)
Avec w(t) strictement positive
Démontrer qu'il existe une unique suite de polynôme

orthonormés telle que:
Pn soit de degrés n
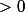
J'ai donc pris
 = t^n)
et P

un polynome de degres n mais je vois pas comment montrer ce qu'ils veulent
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 28 Oct 2008, 20:01
par Purrace » 28 Oct 2008, 20:01
Pour l'orthonormalistion, ton ami est monsieur Schmidt et son procédé
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 28 Oct 2008, 20:09
par muse » 28 Oct 2008, 20:09
et pour montrer ça ?
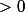
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 28 Oct 2008, 20:26
par Purrace » 28 Oct 2008, 20:26
Cette condition équivaut à ce que le coefficient dominant de t'est polynome est >0 .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités