Bonsoir à tous,
Est ce que quelqu'un pourrait m'aider à comprendre la résolution de cette exercice s'il vous plait?
Il s'agit de calculer les coefficients du polynôme Pn = (1 + X + X2 + ··· + Xn)^2
Pour k ∈ ~0,n, le coefficient de Xk dans Pn est :
a0ak + a1ak−1 + ··· + ak−1a1 + aka0 = k + 1.
Pour le cas k ∈ ~n + 1,2n, on note :
an+1 = ··· = a2n = 0,
de sorte que le coefficient de Xk dans Pn puisse être écrit :
a0ak + ··· + ak−n−1an+1 + ak−nan + ak−n+1an−1 + ···
+ an−1ak−n+1 + anak−n + an+1ak−n−1 + ··· + aka0,
c’est-à-dire :
0 + ak−nan + ··· + anak−n + 0 = n − (k − n) + 1
donc le coefficient est 2n − k + 1
Je comprends la suite du raisonnement mais pas la distinction de cas, ni comment on a trouvé k+1.
Merci pour votre aide!
Polynome ECS
5 messages
- Page 1 sur 1
Re: Polynome ECS
Bonsoir,
Désolé mais c'est vraiment illisible ce que tu as écrit et moi non plus je ne comprends pas.
Si on note
^2) Alors:
Alors:
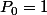
^2 = 1 + 2X + X^2)
^2 = 1 + 2X + 3X^2 + 2X^3 + 1X^4)

Et l'on voit bien, de proche en proche que:

 Jusqu'à ce qu'on arrive "au milieu" cela reste vrai.
Jusqu'à ce qu'on arrive "au milieu" cela reste vrai.
Pour tous les tels que
tels que  , on a
, on a 
Mais lorsque k = n, on a
Et l'on démarre à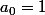 , ce qui te fait
, ce qui te fait  pour k allant de 0 jusqu'à n.
pour k allant de 0 jusqu'à n.
Pour k dans [[0;n]],


Si on veut l'écrire autrement,
* Pour tout k dans [[0 ; n],
* Pour tout k' dans [[n+1; 2n]],
En posant k' = 2n - k
 + 1) puisque k c'est 2n - k' dans notre réindexation
puisque k c'est 2n - k' dans notre réindexation
Désolé mais c'est vraiment illisible ce que tu as écrit et moi non plus je ne comprends pas.
Si on note
Et l'on voit bien, de proche en proche que:
Pour tous les
Mais lorsque k = n, on a
Et l'on démarre à
Pour k dans [[0;n]],
Si on veut l'écrire autrement,
* Pour tout k dans [[0 ; n],
* Pour tout k' dans [[n+1; 2n]],
En posant k' = 2n - k
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Polynome ECS
Salut,
La formule théorique du produit de deux polynômes te dit que, si et
et  (où les
(où les  et les
et les 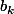 sont nuls à partir d'un certain rang)
sont nuls à partir d'un certain rang)
alors où, pour tout
où, pour tout 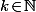 , on a
, on a  .
.
Ici, ce qui signifie que
ce qui signifie que  pour
pour 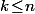 et
et  pour
pour  et, clairement, dans la formule
et, clairement, dans la formule  , il va falloir distinguer différents cas :
, il va falloir distinguer différents cas :
1) Si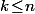 alors, pour tout
alors, pour tout  on a
on a  et, comme
et, comme  est lui aussi dans
est lui aussi dans  on a
on a  ce qui signifie que
ce qui signifie que  .
.
2) Si alors, pour tout
alors, pour tout  on a
on a  uniquement lorsque
uniquement lorsque  et
et  uniquement lorsque
uniquement lorsque  , c'est à dire
, c'est à dire  . Donc
. Donc  uniquement lorsque
uniquement lorsque  (et
(et  sinon).
sinon).
2.a) Si c'est à dire si
c'est à dire si  alors
alors \!+\!1\!=\!2n\!+\!1\!-\!k)
2.b) Si c'est à dire si
c'est à dire si  il n'y a évidement aucun
il n'y a évidement aucun  tels que
tels que  donc
donc 
La formule théorique du produit de deux polynômes te dit que, si
alors
Ici,
1) Si
2) Si
2.a) Si
2.b) Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynome ECS
Ben314,
Merci pour ta réponse! Le rappel du cours éclaire beaucoup, toutefois je ne comprends pas pourquoi tu as distingué le cas ou m serait inférieur à n, n étant le degré du plus grand monôme...
Merci pour ta réponse! Le rappel du cours éclaire beaucoup, toutefois je ne comprends pas pourquoi tu as distingué le cas ou m serait inférieur à n, n étant le degré du plus grand monôme...
Re: Polynome ECS
J'ai modifié les indices pour que ça "colle" mieux avec les notations de ton exo (avec des a_k).
Et si la question, c'est pourquoi on distingue dès le départ le cas k<=n ?
La réponse est : on peut évidement ne pas commencer par distinguer ce cas et directement écrire que, dans absolument tout les cas, on a) .
.
Sauf que, arrivé à ce point, il ne faut pas oublier que il ne varie "que" de 0 à
il ne varie "que" de 0 à  , c'est à dire que
, c'est à dire que ) et là, il faut regarder comment se "combinent" les inégalités (1) et (2) ce qui revient à regarder comment sont placées leurs extrémités les une par rapport aux autres.
et là, il faut regarder comment se "combinent" les inégalités (1) et (2) ce qui revient à regarder comment sont placées leurs extrémités les une par rapport aux autres.
Bilan : il faut donc comparer les "bornes gauches" et
et  ainsi que les "bornes droites"
ainsi que les "bornes droites"  et
et  et ça conduit à distinguer les cas
et ça conduit à distinguer les cas  et
et  : dans le premier cas, c'est l'inégalité (2) qui est plus "restrictive" que la (1) (des deux cotés) et dans l'autre cas, c'est le contraire.
: dans le premier cas, c'est l'inégalité (2) qui est plus "restrictive" que la (1) (des deux cotés) et dans l'autre cas, c'est le contraire.
Si tu y tient vraiment, tu peut écrire une "formule générale" qui dirait que, dans tout les cas, où
où  et
et  (avec la convention que la somme est nulle lorsque
(avec la convention que la somme est nulle lorsque  )
)
Et si la question, c'est pourquoi on distingue dès le départ le cas k<=n ?
La réponse est : on peut évidement ne pas commencer par distinguer ce cas et directement écrire que, dans absolument tout les cas, on a
Sauf que, arrivé à ce point, il ne faut pas oublier que
Bilan : il faut donc comparer les "bornes gauches"
Si tu y tient vraiment, tu peut écrire une "formule générale" qui dirait que, dans tout les cas,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
