Polynôme - divisiblité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 10 Mar 2012, 15:48
par Dinozzo13 » 10 Mar 2012, 15:48
Bonjour j'aimerai prouver ceci :
Soit

où
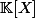
désigne un corps.
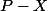
divise

Ca me paraît évident, j'ai fait ce type de raisonnement mais avec des cas particulier en résolvant des équations ! Mais j'ai du mal à le prouver.
Je suis parti d'ici :
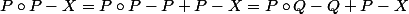
si je pose P=Q, mais je ne parvient pas à conclure correctement :triste:
Merci d'avance pour votre aide
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 10 Mar 2012, 15:52
par ev85 » 10 Mar 2012, 15:52
Dinozzo13 a écrit:Bonjour j'aimerai prouver ceci :
Soit

où
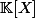
désigne un corps.
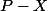
divise

Ca me paraît évident, j'ai fait ce type de raisonnement mais avec des cas particulier en résolvant des équations ! Mais j'ai du mal à le prouver.
Je suis parti d'ici :
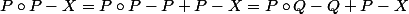
si je pose P=Q, mais je ne parvient pas à conclure correctement :triste:
Merci d'avance pour votre aide
Bonjour.
Que peux-tu de dire de la structure de l'ensemble des polynômes P qui vérifient cette propriété ?
amicalement,
e.v.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 10 Mar 2012, 15:59
par Dinozzo13 » 10 Mar 2012, 15:59
K est un corps donc :
-

est commutative ;
- K possède au moins deux éléments ;
- Tout polynôme non nul de K admet un inverse
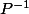
pour

.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 10 Mar 2012, 16:15
par ev85 » 10 Mar 2012, 16:15
Dinozzo13 a écrit: - Tout polynôme non nul de K admet un inverse
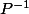
pour

.
Wow !
C'est quoi l'inverse de

? Tu m'avais pas dit qu'on prenait les séries de Puiseux !
e.v.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Mar 2012, 16:16
par Doraki » 10 Mar 2012, 16:16
Dinozzo13 a écrit: - Tout polynôme non nul de K admet un inverse
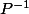
pour

.
euh ° n'est pas une loi de K et les éléments de K ne sont pas des polynômes.
Tu pourrais montrer que pour tous polynômes A,B,C, A°B - A°C est multiple de (B-C) ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 10 Mar 2012, 16:29
par Dinozzo13 » 10 Mar 2012, 16:29
Je voulais dire K[X].

est divisible par B-C car si on prends
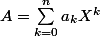
, on a :
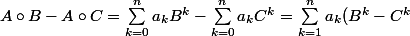)
Or on sait que
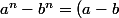\sum_{k=0}^n a^{n-k-1}{ b^k})
donc ...
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 10 Mar 2012, 16:32
par Dinozzo13 » 10 Mar 2012, 16:32
ev85 a écrit:Wow !
C'est quoi l'inverse de

? Tu m'avais pas dit qu'on prenait les séries de Puiseux !
e.v.
Série de Puiseux ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Mar 2012, 16:37
par Doraki » 10 Mar 2012, 16:37
Tu voulais dire que K[X] muni de + et ° est un corps ????
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 10 Mar 2012, 16:41
par ev85 » 10 Mar 2012, 16:41
Dinozzo13 a écrit:Série de Puiseux ?
Ben oui, tu n'as pas
Wikipedia chez toi ?
e.v.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 10 Mar 2012, 16:55
par Dinozzo13 » 10 Mar 2012, 16:55
Doraki a écrit:Tu voulais dire que K[X] muni de + et ° est un corps ????
Ben normalement c'est

, mais ici

intervient
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Mar 2012, 17:02
par Doraki » 10 Mar 2012, 17:02
Sauf que (K[X],+,*) n'est pas un corps, et (K[X],+,°) encore moins.
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 10 Mar 2012, 17:50
par Maxmau » 10 Mar 2012, 17:50
Dinozzo13 a écrit:Bonjour j'aimerai prouver ceci :
Soit

où
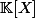
désigne un corps.
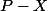
divise

Ca me paraît évident, j'ai fait ce type de raisonnement mais avec des cas particulier en résolvant des équations ! Mais j'ai du mal à le prouver.
Je suis parti d'ici :
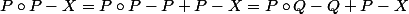
si je pose P=Q, mais je ne parvient pas à conclure correctement :triste:
Merci d'avance pour votre aide
Bj
Ce serait pas P(X) - X divise P(P(X)) - P(X) ??
au temps pour moi, ton énoncé est bon (le mien aussi d'ailleurs)
Pour démontrer ton résultat, travaille modulo P(X) - X pour réduire P(P(X)) - X
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
où
désigne un corps.
divise
si je pose P=Q, mais je ne parvient pas à conclure correctement :triste:
où
désigne un corps.
divise
si je pose P=Q, mais je ne parvient pas à conclure correctement :triste: