Bonjour à tous,
Je bloque désespérément sur un exercice :
"Soit le polynôme x^4 + 14x^2 − 34x − 14. Trouver une racine au moins double à ce polynôme."
J'ai tenté la méthode Ferrari sans résultat...
Avez-vous une idée ?
Polynôme de degré 4
10 messages
- Page 1 sur 1
Re: Polynôme de degré 4
Bonjour,
sais tu comment chercher les racines rationnelles de ce polynôme ?
Edit : je pense qu'il y a une erreur de recopie car ce polynôme n'a pas de racine double
sais tu comment chercher les racines rationnelles de ce polynôme ?
Edit : je pense qu'il y a une erreur de recopie car ce polynôme n'a pas de racine double
Re: Polynôme de degré 4
Je confirme : pas de racines communes entre le polynôme et son polynôme dérivé .
Re: Polynôme de degré 4
Bonjour et merci pour vos réponses.
Je vais vérifier tout ça et vous fait un retour !
Cdt
Je vais vérifier tout ça et vous fait un retour !
Cdt
Re: Polynôme de degré 4
Salut,
Il n'y a pas de racines double ...
P(x) = x^4 + 14x^2 − 34x − 4.
Recherche d'une éventuelle racine entière ...
Si il y a une racine dans Z, c'est obligatoirement un diviseur de 4 (au signe près).
Donc les candidats sont : 1 , 2 et 4 (et les mêmes en négatif)
On essaie et on trouve que P(2) = 0 ... donc x^4 + 14x^2 − 34x − 4 est divisible par (x-2)
On fait la division euclidienne de x^4 + 14x^2 − 34x − 4 par (x-2) et on obtient :
x^4 + 14x^2 − 34x − 4 = (x-2).(x³+2x²+18x+2)
Résolution de x³+2x²+18x+2 = 0 (Méthode de Cardan)
Poser x = y - 2/3
x² = y² + 4/9 - 4/3.y
x³ = y³ + 4/3 y - 2.y² - 8 /27
x³+2x²+18x+2 = 0
y³ + 4/3 y - 2.y² - 8 /27 + 2.(y² + 4/9 - 4/3.y) + 18(y-2/3) + 2 = 0
y³ - 4/3 y - 8 /27 + 8 /9 + 18y - 12 + 2 = 0
y³ + 50/3 y - 254 /27 = 0
p=50/3 , q = -254 /27
(q/2)² + (p/3)³ = (254/27)² + (50/3)³ > 0 --> 1 racine réelle et 2 racines complexes conjuguées qui sont :
^2+(\frac{p}{3})^3}}+\sqrt[3]{-\frac{q}{2}-\sqrt{(\frac{q}{2})^2+(\frac{p}{3})^3}})
Il y a aussi 2 racines complexes conjuguées :
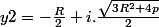
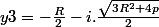
On repasse ensuite aux valeurs de x par x = y - 2/3 ...
Remarque, si il n'y avait pas eu de racine entière "évidente", la méthode de Ferraris permettait de trouver les racines ... mais c'est un peu plus long.

Il n'y a pas de racines double ...
P(x) = x^4 + 14x^2 − 34x − 4.
Recherche d'une éventuelle racine entière ...
Si il y a une racine dans Z, c'est obligatoirement un diviseur de 4 (au signe près).
Donc les candidats sont : 1 , 2 et 4 (et les mêmes en négatif)
On essaie et on trouve que P(2) = 0 ... donc x^4 + 14x^2 − 34x − 4 est divisible par (x-2)
On fait la division euclidienne de x^4 + 14x^2 − 34x − 4 par (x-2) et on obtient :
x^4 + 14x^2 − 34x − 4 = (x-2).(x³+2x²+18x+2)
Résolution de x³+2x²+18x+2 = 0 (Méthode de Cardan)
Poser x = y - 2/3
x² = y² + 4/9 - 4/3.y
x³ = y³ + 4/3 y - 2.y² - 8 /27
x³+2x²+18x+2 = 0
y³ + 4/3 y - 2.y² - 8 /27 + 2.(y² + 4/9 - 4/3.y) + 18(y-2/3) + 2 = 0
y³ - 4/3 y - 8 /27 + 8 /9 + 18y - 12 + 2 = 0
y³ + 50/3 y - 254 /27 = 0
p=50/3 , q = -254 /27
(q/2)² + (p/3)³ = (254/27)² + (50/3)³ > 0 --> 1 racine réelle et 2 racines complexes conjuguées qui sont :
Il y a aussi 2 racines complexes conjuguées :
On repasse ensuite aux valeurs de x par x = y - 2/3 ...
Remarque, si il n'y avait pas eu de racine entière "évidente", la méthode de Ferraris permettait de trouver les racines ... mais c'est un peu plus long.
Re: Polynôme de degré 4
Merci beaucoup pour ta réponse plus que complète ! J'ai très bien compris la démarche grâce à toi.
Re: Polynôme de degré 4
Salut,
Si ce qu'on cherche des les racines au moins doubles d'un polynôme P, il est infiniment plus rapide de calculer calculer le PGCD de P et de P' avec l'algorithme d'Euclide (ce qui est facilement faisable quelque soit le degré) plutôt que de chercher les racines de P.
Ensuite, si comme ici le PGCD vaut 1, ben c'est qu'il n'y a pas de racines multiples et c'est fini.
Si ce qu'on cherche des les racines au moins doubles d'un polynôme P, il est infiniment plus rapide de calculer calculer le PGCD de P et de P' avec l'algorithme d'Euclide (ce qui est facilement faisable quelque soit le degré) plutôt que de chercher les racines de P.
Ensuite, si comme ici le PGCD vaut 1, ben c'est qu'il n'y a pas de racines multiples et c'est fini.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynôme de degré 4
Stykame a écrit:Merci beaucoup pour ta réponse plus que complète ! J'ai très bien compris la démarche grâce à toi.
Tant mieux ...
J'ai juste montré comment on pouvait ici trouver les racines ... pour info.
Cependant, comme cela a été dit plusieurs fois, il n'y a pas besoin de chercher les racines pour montrer qu'il n'y a pas de racines doubles.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
