Polynôme complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
maths0805
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Sep 2018, 13:45
-
 par maths0805 » 29 Oct 2018, 11:09
par maths0805 » 29 Oct 2018, 11:09
Bonjour j'ai besoin de votre aide pour un exercice sur lequel je bloque
n∈N*, on a P(X) = X^n + a
n-1 X^n-1 + ... + a
1 X + a
0P est un polynôme à coefficients complexes
On a z une racine de P, qui peut être complexe
On pose M=max
(0<=k<=n-1) (|a
k|)
La question est : Mq |z|<= 1+M
Merci d'avance

-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 29 Oct 2018, 13:41
par MMu » 29 Oct 2018, 13:41
Qui est

..

-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 29 Oct 2018, 14:01
par mehdi-128 » 29 Oct 2018, 14:01
MMu a écrit:Qui est

..

Je pense qu'il a voulu écrire Montrer que et l'a abrévié en Mq
-
maths0805
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Sep 2018, 13:45
-
 par maths0805 » 29 Oct 2018, 14:10
par maths0805 » 29 Oct 2018, 14:10
Bonjour oui c'est montrer que désolé

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Oct 2018, 18:52
par Ben314 » 29 Oct 2018, 18:52
Salut,
Si

est une racine de

alors, si

le résultat est immédiat et, si

, on a
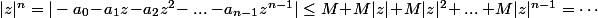
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
maths0805
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Sep 2018, 13:45
-
 par maths0805 » 30 Oct 2018, 09:34
par maths0805 » 30 Oct 2018, 09:34
Ben314 a écrit:Salut,
Si

est une racine de

alors, si

le résultat est immédiat et, si

, on a
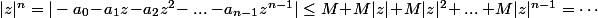
Ce qui est à droite c'est une possibilité du polynôme P c'est ça ?
Mais je vois pas où on peut en venir à 1+M

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Oct 2018, 16:51
par Ben314 » 30 Oct 2018, 16:51
maths0805 a écrit:Ce qui est à droite c'est une possibilité du polynôme P c'est ça ?
Je comprend rien : à droite de quoi ? Tu veut dire quoi par "une possibilité du polynôme P" ?
Si tu parle de la majoration de mon post, ben c'est du débile de débile : le module d'une somme, c'est plus petit que la somme des modules ; le module d'un produit, c'est le produit des modules et, par hypothèse, tout les

ont un module

.
Ensuite, concernant ce qu'il faut écrire ensuite, ben faudrait peut-être avoir un vague souvenir du cours de première sur "la somme des n premiers termes d'une suite géométrique".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
maths0805
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Sep 2018, 13:45
-
 par maths0805 » 31 Oct 2018, 11:29
par maths0805 » 31 Oct 2018, 11:29
Ben314 a écrit: maths0805 a écrit:Ce qui est à droite c'est une possibilité du polynôme P c'est ça ?
Je comprend rien : à droite de quoi ? Tu veut dire quoi par "une possibilité du polynôme P" ?
Si tu parle de la majoration de mon post, ben c'est du débile de débile : le module d'une somme, c'est plus petit que la somme des modules ; le module d'un produit, c'est le produit des modules et, par hypothèse, tout les

ont un module

.
Ensuite, concernant ce qu'il faut écrire ensuite, ben faudrait peut-être avoir un vague souvenir du cours de première sur "la somme des n premiers termes d'une suite géométrique".
D'accord merci je n'avais pas compris comme ça
J'ai donc simplifié la majoration par M*(1-|z|^n)/(1-|z|)
Puis-je faire ce que j'ai eu comme idée ?
Je vous l'explique :
J'ai simplifié M*(1-|z|^n)/(1-|z|) par M*|z|^n-1 car (1-|z|^n)/(1-|z|)~(|z|^n)/|z|=|z|^n-1 car leur rapport tend vers 1
J'obtiens donc :
|z|^n <= M * |z|^n-1
Donc |z| <= M
On a alors |z| <= M+1
Est-ce correct d'écrire cela ?
Merci
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 31 Oct 2018, 12:37
par jlb » 31 Oct 2018, 12:37
Euh,...……………. non!!!!!!!!!!!!!!!!!!! Ce n'est pas une bonne idée! Penses-tu vraiment que lorsque n tend vers l'infini 1 - |z| équivaut à |z|?
Si on reprend |z^n| < M*(|z|^n -1)/(|z| -1), ça, c'est correct! Ton objectif c'est d'obtenir une majoration de |z|, du coup ce serait pas con d'essayer de l'isoler!!
-
maths0805
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Sep 2018, 13:45
-
 par maths0805 » 31 Oct 2018, 13:50
par maths0805 » 31 Oct 2018, 13:50
Merci cette fois-ci est la bonne ! Je tombe bien sur |z| <= M+1
Merci beaucoup !!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
..
est une racine de
alors, si
le résultat est immédiat et, si
, on a
ont un module
.