Polynôme à coefs entiers

par **Nightmare** » 12 Déc 2009, 16:36

En fait je crois que je suis allé un peu vite en disant que les phi(j) laissaient P_p invariant, ça ne me semble pas direct.

par **Nightmare** » 12 Déc 2009, 17:04

Nightmare a écrit:En fait je crois que je suis allé un peu vite en disant que les phi(j) laissaient P_p invariant, ça ne me semble pas direct.

C'est idiot, c'est clair pas construction puisque F est invariant pour les phi(j).

par **ffpower** » 12 Déc 2009, 17:39

Ben314 a écrit:Sauf que je voudrait bien que tu me donne un complexe de module 1 racine d'un polynôme à coeff entiers qui ne soit pas une racine de l'unité.

Ca par contre on peut. Si on prend

tel que

par exemple,

est algébrique de module 1 et n est pas une racine de l unité

par **yos** » 13 Déc 2009, 10:29

Nightmare a écrit:Il reste à prouver que Pp est à coef entiers. Un peu de théorie des corps :

Je considère l'extension finie et k son degré sur Q. On considère par la suite les k automorphismes de corps . Rapidement, on montre que ces automorphismes laissent les Pp invariant et de ce fait ces derniers sont à coef dans Q. Or les (xi) étant algébriques sur Z, il en va de même pour les xi^p et donc les coefs de Pp sont entiers.

Il faut prouver qu'ils sont entiers sur Z et pas seulement algébriques.
De plus "algébrique" signifie que les

sont racine d'un polynôme à coefs entiers, qui n'est pas nécessairement

.
Je pense que ton truc marche mais qu'il faut éclaircir certains détails (mais peut-être que j'ai pas tout suivi dans tes arguments).

Je pense qu'on peut faire ainsi :
En fait, on peut se limiter aux polynômes P irréductibles. Du coup les

sont tous conjugués et les

sont déterminés par certaines permutations des

. Par suite les

sont conjugués également (entre eux, via les

) et donc le polynôme minimal de l'un d'eux les a tous pour racines : c'est donc

.

par **Ben314** » 13 Déc 2009, 12:58

Il me semble que, pour la fin de la preuve, le plus simple est de dire que les coeff. du polynome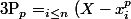

sont les polynômes symétriques élémentaires en les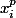

donc sont des polynômes symétriques à coeff. dans

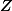en les

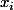donc des polynôme à coeff. dans

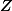des coeffs. du polynôme de départ i.e. des entiers.

En espérant que je n'ai pas (re)dit une connerie.

P.S. Existe t'il un complexe de module 1 racine d'un polynôme unitaire à coeff entiers qui ne soit pas une racine de l'unité ?

par **Doraki** » 13 Déc 2009, 14:50

Si P est un polynôme unitaire à coefficients entiers, le polynôme Q dont les racines sont les carrés des racines de P, est de même degré que P et toujours unitaire à coefficients entiers.

L'ensemble des polynômes unitaire à coefficients entiers dont toutes les racines sont dans le disque unité d'un degré donné est fini,
Donc si P a toutes ses racines dans le disque unité, il faut que toutes ses racines soit des racines de l'unité.

Je sais pas, pour la question de Ben314.

par **Nightmare** » 13 Déc 2009, 15:08

yos a écrit:Il faut prouver qu'ils sont entiers sur Z et pas seulement algébriques.
De plus "algébrique" signifie que les sont racine d'un polynôme à coefs entiers, qui n'est pas nécessairement .
Je pense que ton truc marche mais qu'il faut éclaircir certains détails (mais peut-être que j'ai pas tout suivi dans tes arguments).

Je développe un peu :

On a Pp dans Q[X]. Or, P est dans Z[X], les x_i étant des entiers algébriques, il en va de même pour les xi^p. On en déduit que les coefs de Pp sont des rationnels entiers algébriques sur Z et donc que ce sont des entiers !

par **Nightmare** » 13 Déc 2009, 15:22

En fait le point très peu clair de ma démo est que Pp est à coefficients rationnels.

Cela vient simplement du fait que les rationnels sont les points fixes par tous les k automorphismes F->C. C'est clair car si on prend x dans F fixe par tous les

, ,

, et donc

.

par **ffpower** » 13 Déc 2009, 16:06

Ben314 a écrit:P.S. Existe t'il un complexe de module 1 racine d'un polynôme unitaire à coeff entiers qui ne soit pas une racine de l'unité ?

Ok, autrement dit, existe-t il des entiers algébriques de module 1. La il faut peauffiner un peu. L'ensemble des entiers algébriques est un anneau stable par racine carrée. Si on part d'un entier algébrique quelconque de [-1,1] ( par exemple

), qu'on l'écrit

, alors la relation

assure que

est aussi un entier algébrique, et par suite

est lui aussi un entier algébrique.

par **yos** » 13 Déc 2009, 16:06

Doraki a écrit:Si P est un polynôme unitaire à coefficients entiers, le polynôme Q dont les racines sont les carrés des racines de P, est de même degré que P et toujours unitaire à coefficients entiers.

C'est curieux car si on applique ton cas particulier (exposants 2), on a la finitude de l'ensemble des

(où z est une racine de P) donc une relation du type

avec q0 divise un entier de la forme

. Cela ne me saute pas aux yeux a priori et à vous?

En tout cas, se limiter aux exposants 2 est pas mal car la propriété citée par Ben sur les polynômes symétriques est pas triviale dans le cas général (j'avais fait ça aussi, mais c'est vrai qu'un argument plus arithmétique comme celui de Nightmare montre mieux ce qui se passe).

par **yos** » 13 Déc 2009, 16:08

Ben314 a écrit:Existe t'il un complexe de module 1 racine d'un polynôme unitaire à coeff entiers qui ne soit pas une racine de l'unité ?

Je comprends pas : on vient de prouver que non et on peut même remplacer "module 1" par "module

".

EDIT. Ah non j'ai compris mon erreur: il faudrait que tous ses conjugués soit de module

.

par **ffpower** » 13 Déc 2009, 16:09

yos a écrit:...cela signifie que tout entier m>0 divise un entier de la forme . Cela ne me saute pas aux yeux a priori et à vous?

Ca a l air d etre une conséquence du petit théoreme de Fermat ça

par **Ben314** » 13 Déc 2009, 16:11

Il me semble qu'ici, l'hypothèse était que TOUTES les racines du polynôme sont de module inférieur à 1.
Dans ma question, il n'y en a à priori qu'UNE dont le module est égal à 1...

par **ffpower** » 13 Déc 2009, 16:11

yos a écrit:Je comprends pas : on vient de prouver que non et on peut même remplacer "module 1" par "module ".

Non, on vient de prouver ( enfin plutôt "vous" venez de prouver :we: ) qu'il n y avait pas de polynome unitaire a coeff entiers dont TOUTES les racines sont de module inferieur a 1
EDIT: doublé :lol5:

par **yos** » 13 Déc 2009, 16:13

Pardon, pardon, pardon, mea culpa,

par **Ben314** » 13 Déc 2009, 16:14

Une petite question,
pourquoi l'argument avec les polynômes symétrique élémentaires ne vous va pas ?
Il me parrait bien plus naturel que les extentions de corps ici...

par **yos** » 13 Déc 2009, 16:29

Si ça va mais j'ai un mauvais souvenir de la preuve du théorème en question. Faudrait que je la relise.

Polynôme à coefs entiers

Qui est en ligne