Elle m'intéresse, je n'ai pas raisonné ainsi.
Voici comment j'ai fait rapidement :
Je note (xi) mes racines de module inférieur à 1. Je note
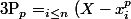)
pour p quelconque. Mon idée est la suivante :
Supposons qu'on puisse prouver que P_p soit lui même à coef entier. L'ensemble des
)
pour p variant dans N est fini et on peut trouver une suite strictement croissante d'entiers
)
telle que
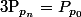
pour tout n.
Quelque soit k, on a donc l'existence d'une permutation

de

telle que
}^{p_{0}})
. Vu qu'on a exactement n! permutation, on peut trouver un entier k' tel que

et
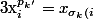}^{p_{0}})
et donc

et c'est donc que xi est une racine de l'unité.
Il reste à prouver que Pp est à coef entiers. Un peu de théorie des corps :
Je considère l'extension finie
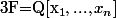
et k son degré sur Q. On considère par la suite les k automorphismes de corps
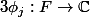
. Rapidement, on montre que ces automorphismes laissent les Pp invariant et de ce fait ces derniers sont à coef dans Q. Or les (xi) étant algébriques sur Z, il en va de même pour les xi^p et donc les coefs de Pp sont entiers.
En espérant n'avoir pas trop raconté de bêtises !
