Polynome caractéristique.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mohamed
- Membre Relatif
- Messages: 225
- Enregistré le: 02 Juil 2006, 21:01
-
par Mohamed » 19 Aoû 2007, 21:20
Bonsoir
A une matrice de
)
=)
det(
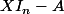
) (le polynome caractéristique de A)
d'abord est ce ces résultats sont justes?
le coeff dominant: je trouve 1
.........de degré (n-1) ...tr(A)
Après on me demande de prouver que le coff du terme de degré n-k
est
^kd_k)
ou
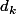
est la somme de tous les sous déterminants d'ordre k extraits de A
là je bloque totalement..veuillez m'aider svp
Merci d'Acance+
-
achille
- Membre Naturel
- Messages: 94
- Enregistré le: 27 Juin 2007, 11:21
-
par achille » 19 Aoû 2007, 22:02
d'abord je croit que le Polynôme caractéristique est de degré n est le coef dominant est (-1)^n, à vérifier...
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
par kazeriahm » 19 Aoû 2007, 23:14
salut
ca ca dépend de la définition qu'on comprend.
Avec celle donnée par Mohamed c'est bon. On peut aussi définir le polynome caractéristique par P(x)=|M-x*I| ce qui alors donne un coefficient dominant (-1)^n.
Pour ta question mohamed,
note Ci la i ème colonne de ta matrice M.
P(x)=|(x*e1-C1,x*e2-C2,...,x*en-Cn)|
Tu utilises alors la n-linéarité du déterminant pour développer cette expression
et trouver le résultat...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
