Polynome caractéristique

par **antoine3617** » 30 Nov 2006, 12:03

bonjour,

pouvez-vous m'aider svp ?
soit E un espace vectoriel de dimension 2.u et v sont deux endomorphismes de E vérifiant la propriété :
uov-vou=u.
on suppose u non nul
j'ai trouvé déjà que u n'est pas bijectif,la matrice de u^2, puis la dimension de Ker u,puis Ker u est stable par v et je n'arrive pas à montrer que lorsque K=R , toutes les racines du polynome caractèristique de v sont réelles.
merci par avance

par **yos** » 30 Nov 2006, 13:26

Bonjour.
Si u pas bijectif, alors det(u)=0, mais comme on a Tr(u)=0 (évident), alors le polynôme caractéristique est X², ce qui veut dire que u²=0.
Est-ce bien compatible avec ce que tu as?

par **antoine3617** » 30 Nov 2006, 14:55

Je ne vois pas trop pourquoi le poly car est x^2 ,pour le reste c'est ok mais tu écris le poly caractéristique de u et on nous parle de celui de v .
D'après la formulation de la question dans l'énoncé, il faut déduire du fait que ker u est stable par v que toutes les racines du poly caract de v sont réelles.
Je ne vois pas trop....

par **tize** » 30 Nov 2006, 15:14

Le polynôme caractéristique de u est X² car en dimension 2 le polynôme caractéristique est : X²-Tr(u)X+det(u) et dans ton cas précis Tr(u)=det(u)=0

par **antoine3617** » 30 Nov 2006, 15:39

merci pour la formule,ça me revient maintenant.
Si quelqu'un peut m'aider pour mon problème de base à savoir :
déduire du fait que ker u est stable par v que les racines du polynome caractéristisque de v sont réelles sachant que l'on travaille dans le corps des réels.

par **tize** » 30 Nov 2006, 16:46

Je ne suis pas très sur, à vérifier:
Soit

un vecteur propre de associé à la valeur propre

et

et tel que

. C 'est possible puisque les espaces propres sont en somme direct et

. On a avec l'hypothèse :

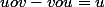donc

d'ou

et puisque

(car

) on en déduit qu'alors

est aussi une valeur propre de v dans un espace de dimension 2. Les seuls valeurs propres de v sont donc

et

. Or si le corps de base est

alors le polynôme caractéristique de v est à coefficient réel, ses racines sont donc (si elles sont complexes) conjuguées, or

et

ne sont jamais conjuguées donc

et

sont réelle !

par **abcd22** » 30 Nov 2006, 17:22

Bonjour,
On travaille dans un espace vectoriel de dimension 2, Ker u est non nul car u n'est pas bijectif, ce n'est pas l'espace entier car u est non nul, c'est donc une droite, et on a montré qu'elle est stable par v, donc tout élément non nul de Ker u est un vecteur propre de v pour une valeur propre réelle. Comme la somme des valeurs propres de v est réelle, on en déduit que la 2e valeur propre de v est réelle.

par **tize** » 30 Nov 2006, 17:25

C'est beaucoup plus élégant comme ça, merci abcd22 ! :we:

par **antoine3617** » 02 Déc 2006, 13:42

C'est bon pour ce passage et merci encore pour l'aide précieuse.
Voici la suite du problème pour laquelle j'ai de nouveau des difficultés:
on a formé la base suivante (a,u(a)).J'ai déterminé a de E tels que (a,u(a))soit une base de E.
si a n'appartient pas à ker u alors (a,u(a)) est une base de E.soit B la base ainsi constituée.

1)determiner par leurs matrices relativement à B les éléments w tels que (u,w) ait la propriété uow-wou=u
soit W l'ensemble qu'ils constituent.
2)montrer que les éléments de W sont tous diagonalisables.

Est-ce que la matrice de u relativement à B (a,u(a)) est bien
[0 0]
[1 0]
??
merci d'avance

par **abcd22** » 02 Déc 2006, 14:19

antoine3617 a écrit:Est-ce que la matrice de u relativement à B (a,u(a)) est bien
[0 0]
[1 0]
??

Oui c'est ça.

par **antoine3617** » 02 Déc 2006, 18:24

c'est bon j'ai trouvé les éléments w qui vérifient la propriété.

J'ai d'autres problèmes un peu plus loin.Si vous pouvez m'aider svp :
on ne suppose plus que n=2
j'ai démontré la propriété suivante : u^(k)ov-vou^(k)=ku^(k) pour tout entier k strictement positif.
on se propose de montrer que u^n est l'endomorphisme nul.Supposons que la dimension de Im u^n ne soit pas nulle.
1)montrer que Im u^n est stable par u^n et v
2)désignant par f et g les endomorphismes induits respectivement par u^n et v sur Im u^n,montrer que f est bijectif,exprimer fog-gof en fonction de f et en déduire une contradiction.Conclure.Quel est alors Ker u^n ?

J'ai en partie démontré le 1) mais je ne sais pas si c'est valide :
soit y app Im u^n.alors il existe x app E tel que u^n(x)=y

u^n o u^n(x)=u^n(y)
u^n(x) app E d'où u^n(y) app Im u^n
et Im u^n est stable par u^n

v o u^n(x)=v(y)
(d'après la propriété) u^(n)ov(x)-ku^n(x)=v(y)
u^(n)ov(x)-ky=v(y)
or v(x) app E d'où u^(n)ov(x) app Im u^n
-ky app Im u^n
alors v(y) app Im u^n
Im u^n est stable par v
Qu'en pensez-vous ?

par **antoine3617** » 03 Déc 2006, 23:49

voici mon problème, si quelqu'un peut m'aider,ça serait super

on ne suppose plus que n=2
j'ai démontré la propriété suivante :
u^(k)ov-vou^(k)=ku^(k) pour tout entier k strictement positif.
on se propose de montrer que u^n est l'endomorphisme nul.Supposons que la dimension de Im u^n ne soit pas nulle.

Désignant par f et g les endomorphismes induits respectivement par u^n et v sur Im u^n,montrer que f est bijectif,exprimer fog-gof en fonction de f et en déduire une contradiction.Conclure.Quel est alors Ker u^n ?

merci par avance

par **antoine3617** » 05 Déc 2006, 19:32

help !!!!
merci d'avance à tous ceux qui peuvent m'aider, même si ce n'est qu'une indication.

par **antoine3617** » 07 Déc 2006, 16:43

bonjour,

il me manque plus qu'à montrer que f est bijectif .comment faire ?
ensuite, j'ai montré que fog - gof=nf et je dois en déduire une contradiction.Et là je peine.j'ai essayé avec la dimension.on avait supposé que la dimension de u^n n'était pas nulle.

merci par avance

par **fahr451** » 07 Déc 2006, 17:55

si j'ai bien compris le pb c 'est u,v deux endo de E, E de dim finie n vérifiant
u°v-v°u = u montrer que u^n = 0?
tu as montré pour tout k entier

u^k° v - v°u^k = k u^k

maintenant en considérant l 'endomorphisme h de L(E)
w ->w°v-v°w si pour tout k u^k était non nul

u^k serait vecteur propre de h associé à la valeur propre k et donc h aurait une infinité de valeurs propres c'est absurde car h est un endo en dim finie ( n^2) donc il existe une puissance nulle de u et ensuite il est classique que u^n = 0 ( n = dim E)

par **yos** » 07 Déc 2006, 18:05

Bonsoir.
Il faudrait que je revois le truc depuis le début. C'est possible d'avoir l'énoncé intégral? Par mail éventuellement.
Pour la contradiction à mettre en évidence tu ne peux pas utiliser la même méthode qu'à la première question où tu as prouvé que u n'est pas bijectif? D'ailleurs t'as fait comment?
Un peu plus loin, Tize montre que si

est vp de v pour un vecteur propre pas dans ker u, alors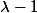

est aussi vp de v. Ceci est valable hors de la dimension 2, mais ça entraînerait une infinité de valeurs propres par itération du procédé, ce qui est impossible, à moins que les vecteurs propres finissent dans ker u. A toi de voir si ça peut te servir. J'ai pas une vision globale. Si tu t'en sors pas, il me faudrait le sujet pour t'en dire plus.

par **antoine3617** » 09 Déc 2006, 18:18

Je peux te l'envoyer par mail.Donne moi ton adresse

par **antoine3617** » 11 Déc 2006, 23:39

on ne se place plus en dim 2

j'ai montré que ker u^k est stable par v.
comment montrer que les vecteurs non nuls de ker u sont vecteurs propres de v et en déduire lorsque K=R,que le polynôme caractèristique de v possède au moins une racine réelle ?

par **fahr451** » 12 Déc 2006, 00:05

j'ai déjà répondu à la question u^n = 0

par **yos** » 12 Déc 2006, 15:04

Tu te ramènes au cas n=2 en considérant la restriction de v à Ker u² (qui est de dimension 2).

Polynome caractéristique

polynome caractéristique

Qui est en ligne