Point fixe
29 messages
- Page 1 sur 2 - 1, 2
point fixe
Bonjour
Soit f une fonction dérivable de [a,b] dans R. Soit c un point fixe de f tel que |f'(c)|>1 alors c est un point fixe répulsif.
Quelle est l'idée de la démo pour montrer que si |f'(c)|>1 alors c est répulsif?
merci
Soit f une fonction dérivable de [a,b] dans R. Soit c un point fixe de f tel que |f'(c)|>1 alors c est un point fixe répulsif.
Quelle est l'idée de la démo pour montrer que si |f'(c)|>1 alors c est répulsif?
merci
on a: -f(c)}{x-c}= f'(\theta _x)) , avec
, avec  strictement compris ente
strictement compris ente  et
et  (égalité des accroissements finis), donc puisque
(égalité des accroissements finis), donc puisque  vérifie le théorème des valeurs intermédiaires et est même en général continue, il existe
vérifie le théorème des valeurs intermédiaires et est même en général continue, il existe 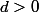 tel que si
tel que si |>1) ; donc si
; donc si  différent de
différent de  est dans
est dans
 , on aura
, on aura -c}{u_n-c}= f'(\theta _U_n)) et donc
et donc
-c|>|U_n-c| |U_{n+1}-c|>|U_n-c|) , donc l'idée, c'est que si un terme se rapproche trop près de c, le suivant s'éloignera de c, ce qui empêche toute convergence. Ce n'est pas très facile à mettre en forme, mais l'idée est là.
, donc l'idée, c'est que si un terme se rapproche trop près de c, le suivant s'éloignera de c, ce qui empêche toute convergence. Ce n'est pas très facile à mettre en forme, mais l'idée est là.
Exemple: et
et  est répulsif et
est répulsif et  attractif; cette suite convergera toujours vers
attractif; cette suite convergera toujours vers (et même très vite car
(et même très vite car=0) )
)
Si on prend) on aura encore un autre cas puisque
on aura encore un autre cas puisque =1) ;
;
En fait le cas attractif est bien plus simple!
Exemple:
Si on prend
En fait le cas attractif est bien plus simple!
zork a écrit:Bonjour
Soit f une fonction dérivable de [a,b] dans R. Soit c un point fixe de f tel que |f'(c)|>1 alors c est un point fixe répulsif.
Quelle est l'idée de la démo pour montrer que si |f'(c)|>1 alors c est répulsif?
merci
Salut,
Il faut donner une définition à "répulsif", non ?
Je dirais par exemple, si je me situe proche de c mais pas en c, alors l'image de ce point par f m'amène plus loin de c...
Après, tout dépend répulsif pour qui, pour ceux proches de c, ou tous les points de [a;b]...
Ou :
Et il y a le lien direct avec la dérivée dans cette expression... Ca fait penser aux accroissements finis...
EDIT : grillé à deux minutes près pfff :zen:
paquito a écrit:vérifie le théorème des valeurs intermédiaires et est même en général continue
On peut prendre quoi comme fonction continue et dérivable mais de dérivée non continue ?
J'ai encore du mal à voir ce que ça pourrait être.
Car ce qui me fait penser au fait que la dérivée n'est pas continue, c'est qu'il y a une "cassure de pente"... donc pas dérivable (au sens fort, pas "ou à gauche ou à droite").
Donc sur les fonctions à 1 seule variable, est-ce possible ?
BiancoAngelo a écrit:Salut,
Il faut donner une définition à "répulsif", non ?
Je dirais par exemple, si je me situe proche de c mais pas en c, alors l'image de ce point par f m'amène plus loin de c...
Après, tout dépend répulsif pour qui, pour ceux proches de c, ou tous les points de [a;b]...si je traduis ce que j'ai écrit.
Ou :
Et il y a le lien direct avec la dérivée dans cette expression... Ca fait penser aux accroissements finis...
EDIT : grillé à deux minutes près pfff :zen:
Pas grillé quand même! :ptdr: l'idée est la même; mais le problème peut être varié; par exemple avec arctan, si on part de 5, ça décroit puis ça ne bouge plus alors qu'on est encore loin de 0!!!
paquito a écrit:Pas grillé quand même! :ptdr: l'idée est la même; mais le problème peut être varié; par exemple avec arctan, si on part de 5, ça décroit puis ça ne bouge plus alors qu'on est encore loin de 0!!!
Oui... ! :we:
D'ailleurs, pour parler des fonctions aux dérivées non continues, si on prend :
Soit
On a
Et là, on peut pas utiliser la continuité de la dérivée... et même pour les accroissements finis, comme la dérivée prend de grandes valeurs mais aussi zéro, des fois...
BiancoAngelo a écrit:Oui... ! :we:
D'ailleurs, pour parler des fonctions aux dérivées non continues, si on prend :
Soitpour
et
.
On a
Et là, on peut pas utiliser la continuité de la dérivée... et même pour les accroissements finis, comme la dérivée prend de grandes valeurs mais aussi zéro, des fois...
les fonctions dérivées vérifient le théorème des a.f. même si elles sont discontinues, ce qui ne donne pas une solution à ton problème, mais donne un cas de plus à étudier!! :marteau:
paquito a écrit:les fonctions dérivées vérifient le théorème des a.f. même si elles sont discontinues, ce qui ne donne pas une solution à ton problème, mais donne un cas de plus à étudier!! :marteau:
Ah mais je suis d'accord ! Je n'apporte pas de solution :we:
Je dis juste ça par rapport à :
il existetel que si
Dans un cas tordu, faudrait trouver une fonction dont la dérivée serait supérieure à 1 (en valeur absolue) "loin" de la valeur du point fixe, tu me suis ?
Concrètement, ça signifierait que ce point est répulsif seulement quand on est "loin", non ?
Imaginons en plus que ce "loin" soit en dehors de l'intervalle de travail [a;b]... Ca ne fonctionnerait plus.
Du coup, est-ce que ça veut dire qu'il est impossible d'avoir une fonction dérivable sur [a;b] tel qu'il existe un unique c tel que
Oulala... C'était juste l'idée, de pousser la démonstration jusqu'au cas des dérivées non continues en supposant qu'il existe une unique valeur supérieure à 1, à savoir, en ce point fixe...
paquito a écrit:Pour moi, si tu prend le cas rarissime d'une dérivée non continue en un de ses points fixe on vas avoir un problème du type:" tu avances ou tu recules, comment veux tu , comment veux tu que je....."
Sinon |f(c)|>1 et| f'(x)|1 et| f'(x)|1 et| f'(x)|<1 [/TEX]partout ailleurs, c'est impossible.
Je veux bien le croire, j'aimerais en avoir le coeur net.
Pour le démontrer, est-ce qu'on peut dire que :
Pour une notion de dérivée, on est forcé de travailler sur un intervalle de longueur non nulle, sinon ça n'a pas de sens.
Soit I un intervalle ]a;b[ sur lequel la dérivée de f existe en tout point (ie la fonction f est dérivable sur I).
On note
Alors E ne peut pas avoir de point isolé..., voilà ce qu'il faut démontrer. (c'est ça qui finalement me paraît délicat).
Ce que je comprends alors, c'est que la dérivée, si elle est discontinue, alors sa valeur au point de discontinuité doit nécessairement appartenir à l'adhérence de I...
Ce qui expliquerait par ailleurs pourquoi le théorème des a.f. fonctionne aussi pour les dérivées discontinues...
Effectivement une dérivée qui prend une valeur 1 prendra obligatoirement la valeur 1; le seul cas de discontinuité pour une dérivée c'est quand-f(x_0)}{h}) existe
existe ) et que
et que) n'a pas de limite en
n'a pas de limite en  (tu as donné un exemple); sinon on démontre (accroissements finis) que
(tu as donné un exemple); sinon on démontre (accroissements finis) que = \lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h} =f'(x_0)) .
.
D'autre part, on démontre que toutes les dérivées vérifient le théorème des v.i.; la démonstration n'est pas difficile, mais repose sur une fonction auxiliaire que je n'ai plus en tête ( je vais rechercher). en résumé les fonctions dérivées sont très régulières.
D'autre part, on démontre que toutes les dérivées vérifient le théorème des v.i.; la démonstration n'est pas difficile, mais repose sur une fonction auxiliaire que je n'ai plus en tête ( je vais rechercher). en résumé les fonctions dérivées sont très régulières.
paquito a écrit:J'ai regardé un autre cas:on a
, on a
ce qui donnera
, mais comment prouver que
diverge vers
?
Ok d'acc
Comme j'ai loupé une partie de la fin de ma licence de maths, la dérivabilité m'échappe un peu, même si j'essaie de rattraper ça vite.
En tout cas, se dire que la dérivée existe, même que c'est dérivable, à savoir que f(x) existe, mais que la limite f(t) quand t tend vers x n'existe pas, c'est déroutant. Ça sort complètement de l'intuition de base.
Ça rend du coup tout ce bazar super intéressant !
Sinon pour la fonction que tu donnes, tu prends n'importe quel
Et tu prends ce cas car on a 0 comme point fixe répulsif ?
Bonjour Angelo,
Bizarrement, il est parfois plus difficile de montrer qu'une suite diverge que de montrer qu'elle converge; je prends un exemple où ça va bien:
 et
et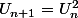 , donc
, donc =x^2) et pour
et pour >2) ; tu as
; tu as -f(1)}{U_n-1}=f'(\epsilon_n)) avec
avec 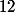 et
et ) ;
;
on en déduit) et puisque
et puisque , la divergence de
, la divergence de  vers
vers 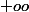 . en fait, je n'ai pas choisi la méthode la plus simple et par exemple on ne pourrait plus faire ça en T°S.
. en fait, je n'ai pas choisi la méthode la plus simple et par exemple on ne pourrait plus faire ça en T°S.
Si je prends= 1,5x+sin(x)) , la méthode précédente tombe à l'eau car
, la méthode précédente tombe à l'eau car \leq 2,5) , mais on arrive à montrer que pour
, mais on arrive à montrer que pour >x) ; on en déduit que
; on en déduit que  est croissante; comme
est croissante; comme ) n'a pas d'autre point fixe que
n'a pas d'autre point fixe que ,
,  ne peux pas être convergente et donc
ne peux pas être convergente et donc  diverge vers
diverge vers 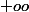 . Mine de rien, ça fait un bon petit exo et ce raisonnement par l'absurde est applicable à l'exemple précédent.
. Mine de rien, ça fait un bon petit exo et ce raisonnement par l'absurde est applicable à l'exemple précédent.
Sinon, on ne nous parle pas de ça au lycée et pas plus à la fac; personnellement, c'est en préparant l'agrégation que j'ai comblé pas mal de lacunes, par exemple: comment on démontre que si f est continue surdt=F(b)-F(a)) .
.
Enfin, si l'on prend=4x^2sin(1/x)) et
et  =0) , si l'on prend
, si l'on prend on constate que ça diverge,
on constate que ça diverge, 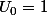 aussi, mais
aussi, mais  , ça converge vers 0, c'est à dire qu'on a un point fixe ni répulsif, ni attractif donc c'est le bordel!!!
, ça converge vers 0, c'est à dire qu'on a un point fixe ni répulsif, ni attractif donc c'est le bordel!!!
Bizarrement, il est parfois plus difficile de montrer qu'une suite diverge que de montrer qu'elle converge; je prends un exemple où ça va bien:
on en déduit
Si je prends
Sinon, on ne nous parle pas de ça au lycée et pas plus à la fac; personnellement, c'est en préparant l'agrégation que j'ai comblé pas mal de lacunes, par exemple: comment on démontre que si f est continue sur
Enfin, si l'on prend
paquito a écrit:Bonjour Angelo,
Bizarrement, il est parfois plus difficile de montrer qu'une suite diverge que de montrer qu'elle converge; je prends un exemple où ça va bien:et
, donc
et pour
; tu as
avec
et
;
on en déduitet puisque
, la divergence de
vers
. en fait, je n'ai pas choisi la méthode la plus simple et par exemple on ne pourrait plus faire ça en T°S.
Si je prends, la méthode précédente tombe à l'eau car
, mais on arrive à montrer que pour
; on en déduit que
est croissante; comme
n'a pas d'autre point fixe que
,
ne peux pas être convergente et donc
diverge vers
. Mine de rien, ça fait un bon petit exo et ce raisonnement par l'absurde est applicable à l'exemple précédent.
Sinon, on ne nous parle pas de ça au lycée et pas plus à la fac; personnellement, c'est en préparant l'agrégation que j'ai comblé pas mal de lacunes, par exemple: comment on démontre que si f est continue sur.
Enfin, si l'on prendet
, si l'on prend
on constate que ça diverge,
aussi, mais
, ça converge vers 0, c'est à dire qu'on a un point fixe ni répulsif, ni attractif donc c'est le bordel!!!
Salut paquito, merci pour ces bons exemples.
En tout cas, c'est quand même agréable de se dire qu'il y a des cas où ce n'est pas stable, qu'on doit faire de l'étude locale pour démontrer les choses, car si on devait toujours tout démontrer à gros coup de canon... :ptdr:
Bizarrement, zork n'a pas réagi suite à nos réponses, pourtant ça fait un bon article pour agrémenter sa question :we:
Tu as raison, on a un peu approfondit la question et ça s'avère intéressant, mais bon......
Sinon, c'est vrai que quand il faut chercher un petit peu, c'est plus satisfaisant que d'appliquer sans réfléchir un résultat de cours :dodo:
Il y a d'autres cas qui sont pas mal non plus comme celui ci donné au concours général:
étudier la convergence de la suite définie par U_0 \geq 0 et .
.
Cette fois ci, en faisant quelques essais, on se rend compte que U_n doit converger vers 1, mais pour des valeurs de assez petites
assez petites  commence par être croissante, ce qui crée la difficulté de l'exercice; si ça t'amuse.... :ptdr:
commence par être croissante, ce qui crée la difficulté de l'exercice; si ça t'amuse.... :ptdr:
Sinon, c'est vrai que quand il faut chercher un petit peu, c'est plus satisfaisant que d'appliquer sans réfléchir un résultat de cours :dodo:
Il y a d'autres cas qui sont pas mal non plus comme celui ci donné au concours général:
étudier la convergence de la suite définie par U_0 \geq 0 et
Cette fois ci, en faisant quelques essais, on se rend compte que U_n doit converger vers 1, mais pour des valeurs de
paquito a écrit:Tu as raison, on a un peu approfondit la question et ça s'avère intéressant, mais bon......
Sinon, c'est vrai que quand il faut chercher un petit peu, c'est plus satisfaisant que d'appliquer sans réfléchir un résultat de cours :dodo:
Il y a d'autres cas qui sont pas mal non plus comme celui ci donné au concours général:
étudier la convergence de la suite définie par U_0 \geq 0 et.
Cette fois ci, en faisant quelques essais, on se rend compte que U_n doit converger vers 1, mais pour des valeurs deassez petites
commence par être croissante, ce qui crée la difficulté de l'exercice; si ça t'amuse.... :ptdr:
Effectivement cette suite, ce n'est pas du gâteau :ptdr:
J'ai pu trouver un résultat proprement :
L'autre résultat, plus intéressant, qui reste à démontrer, que j'ai pu trouver grâce à des tracés graphiques :
BiancoAngelo a écrit:Effectivement cette suite, ce n'est pas du gâteau :ptdr:
J'ai pu trouver un résultat proprement :implique
.
L'autre résultat, plus intéressant, qui reste à démontrer, que j'ai pu trouver grâce à des tracés graphiques :et la suite resterait alors décroissante.
c'est un peu plus compliqué! personnellement,je pensais qu'une démonstration directe aboutirait;que nenni, ii faut faut faire autre chose!
Salut,
personnellement, je suis resté sur une démo directe et impossible d'aboutir!
Ce que l'on peut montrer, c'est que a partir du rang
a partir du rang , donc on peut considérer que
, donc on peut considérer que  est minorée par 1 qui devient la seule limite possible;
est minorée par 1 qui devient la seule limite possible;
d'autre part si pour un entier , on a
, on a , on aura
, on aura  et à fortiori
et à fortiori soit
soit  et
et  sera décroissante à partir du rang
sera décroissante à partir du rang  .
.
Il n'y a donc que 3 cas possibles:
(1) est décroissante et minorée par 1 :ptdr:
est décroissante et minorée par 1 :ptdr:
(2) est unimodale ( d'abord croissante, ensuite décroissante) et minorée par 1 :ptdr:
est unimodale ( d'abord croissante, ensuite décroissante) et minorée par 1 :ptdr:
(3) est croissante :mur:
est croissante :mur:
il y a un cas à éliminer; je te laisse le plaisir de le faire.
personnellement, je suis resté sur une démo directe et impossible d'aboutir!
Ce que l'on peut montrer, c'est que
d'autre part si pour un entier
Il n'y a donc que 3 cas possibles:
(1)
(2)
(3)
il y a un cas à éliminer; je te laisse le plaisir de le faire.
paquito a écrit:Salut,
personnellement, je suis resté sur une démo directe et impossible d'aboutir!
Ce que l'on peut montrer, c'est quea partir du rang
, donc on peut considérer que
est minorée par 1 qui devient la seule limite possible;
d'autre part si pour un entier, on a
, on aura
et à fortiori
soit
et
sera décroissante à partir du rang
.
Il n'y a donc que 3 cas possibles:
(1)est décroissante et minorée par 1 :ptdr:
(2)est unimodale ( d'abord croissante, ensuite décroissante) et minorée par 1 :ptdr:
(3)est croissante :mur:
il y a un cas à éliminer; je te laisse le plaisir de le faire.
Pour l'instant, je galère... Je n'arrive pas à montrer qu'elle ne peut pas rester croissante...
29 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
