Point critique

[selda6958]

donc c'est quoi ?

[selda6958]

donc conclusion ??

[aymanemaysae]

M. ben314 oriente et remet les choses dans le bon ordre quand quelqu'un comme moi dérape, je le remercie bien. Mais pour ne pas nous arrêter, cherchons d'abord les points critiques de g, ensuite on verra.

[Ben314]

Si tu parle de la fonction
f(x,y)=x²+y²-xy
le point (0,0) est bien un minimum global, mais pour le démontrer, il faut forcément faire autre chose que des dérivées partielles.
Par exemple, là, sans le moindre calcul d'une quelconque dérivée, il me semble que c'était pas super dur d'écrire que
f(x,y)=(x-y/2)²+3y²/4 (exactement le même principe que la "mise sous forme canonique" vu en seconde)
et d'en déduire immédiatement que pour tout (x,y) (somme de deux réels positifs) avec égalité ssi x-y/2=0 et y=0, c'est à dire (x,y)=(0,0)

[selda6958]

en cours on a vu un théorème que si c'est un minimum avec la matrice hessienne on fait la trace et trouve le déterminant puis si la fonction est convexe c'est un minimum global

[selda6958]

mais la je n'arrive pas à comprendre pour erreur pour la fonction g

[aymanemaysae]

Puisque M. Ben314 est là, on va profiter de sa présence pour assimiler cette notion d'extremums globaux ou locaux.

on a , donc :

et ,

donc pour x = y, et pour

donc on a , ce qui donne y = 1 ou , donc les points critiques sont (1,1) et ( ) .

Je vous demande de comparer vos résultats avec les miennes, avant de faire appel à M. Ben314 pour la suite de l'exercice.

[selda6958]

du coup j'ai refais mes calculs et je trouve comme vous

[aymanemaysae]

Donc on fait comme au cours, et on établit d'abord la matrice Hessienne.

Établissez votre matrice Hessienne , je ferai de même et on comparera.

[selda6958]

D² f(x,y) = -2 2
2 -6y

du coup le -6 y je peux remplacer par 1/3 ?

[selda6958]

je sais pas si vous avez compris
-2 2
2 -6y

[aymanemaysae]

Bonne réponse.

Maintenant on va prendre le point critique (1,1) , et on va calculer sa matrice Hessienne:

j'ai trouvé ,

et maintenant on va calculer son déterminant et sa trace.

Edit :Il vaut mieux opter pour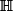 (f) pour désigner la matrice Hessienne.

[selda6958]

du coup cous avez écrit -6 et pas -6 y ce n'est pas pareil non ?

[selda6958]

ah non c'est la matrice au point (1,1) pardon

[selda6958]

je trouve pareil
déterminant 8 et trace -8

[aymanemaysae]

Donc que dit le cours?

[selda6958]

c'est un maximum mais après je ne sais pas comment démontrer que c'est local ou global ?

[aymanemaysae]

Voyons avec notre s'il est local .

[selda6958]

du coup je trouve 16 pour s²-rt

[aymanemaysae]

De plus pour montrer que l'extremum n'est pas global, on peut exhiber un exemple qui met en défaut la globalité de l'extremum: par exemple pour le point (1,1) on a trouvé que c'est un maximum où f prend la valeur 1, mais on peut trouver un point par exemple (0,-10) où la fonction prend une valeur supérieur à ce maximum: ici c'est 990 qui est bien très supérieure à la valeur 1, donc le point (1,1) n'est pas un maximum global.