Point critique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 29 Jan 2016, 21:12
par aymanemaysae » 29 Jan 2016, 21:12
Non!
Vous avez trouvé que
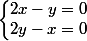

 - x = 0\end{matrix})
j'ai remplacé ici 'y' par '2 x' dans la deuxième ligne.
Trouvez d'abord les valeurs de x et y , après on continuera notre chemin.
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 29 Jan 2016, 21:18
par selda6958 » 29 Jan 2016, 21:18
bah y=2x
4x-x=0 => 3x=0 => x= -3 donc y = 2*(-3)= -6
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 29 Jan 2016, 21:20
par aymanemaysae » 29 Jan 2016, 21:20
Attention à l'erreur : 3x=0 => x= -3 : c'est la même que pour 2 x = y .
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 29 Jan 2016, 21:21
par selda6958 » 29 Jan 2016, 21:21
ah oui x=0
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 29 Jan 2016, 21:23
par selda6958 » 29 Jan 2016, 21:23
donc x=0 et y=0 ?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 29 Jan 2016, 21:31
par aymanemaysae » 29 Jan 2016, 21:31
Brovo!
Vous m'avez fait peur.
Maintenant, nous allons faire comme pour l'exercice 'Optimisation libre' en calculant r, s et t.
Bon courage.
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 29 Jan 2016, 21:39
par selda6958 » 29 Jan 2016, 21:39
dac merci quelques trous de mémoire par moment du coup 0 est mon seul point critique je suppose ?
je posterais mes réponses demain car je vais me reposer un peu trop de maths nuit à la santé

-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 30 Jan 2016, 12:24
par aymanemaysae » 30 Jan 2016, 12:24
Au cas où vous voulez continuer votre exercice, c'est (0,0) le point critique et non 0.
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 30 Jan 2016, 19:32
par selda6958 » 30 Jan 2016, 19:32
pour la fonction f(x) c'est un minimum global
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 30 Jan 2016, 19:39
par selda6958 » 30 Jan 2016, 19:39
pour la fonction g le point critique est (0,0) aussi ?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 30 Jan 2016, 19:50
par aymanemaysae » 30 Jan 2016, 19:50
Oui, bien vu.
On a
 = 2)
,
 = 2)
et
 = - 1)
Donc pour (x,y) = (0,0) on a
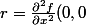 = 2)
,
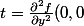 = 2)
, et
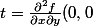 = - 1)
,
donc

et

alors au point (0,0) on a bien un minimum strict .
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 30 Jan 2016, 19:56
par selda6958 » 30 Jan 2016, 19:56
pour la fonction g elle admet un col car dans le cours j'ai vu que f'' x² <0 alors f présente un minimum si le déterminant est > 0, ensuite si le déterminant < 0 f présente un col et si le déterminant =0 on ne peut conclure
du coup ma fonction g admet un col donc il n'y a pas de minimum et maximum si j'ai compris ?
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 30 Jan 2016, 19:57
par aymanemaysae » 30 Jan 2016, 19:57
Pour g , je crois que votre réponse est fausse.
Pouvez-vous me dire comment vous avez procédé?
Edit: ceci concerne votre avant dernière réponse.
Modifié en dernier par
aymanemaysae le 30 Jan 2016, 20:01, modifié 1 fois.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Jan 2016, 20:00
par Ben314 » 30 Jan 2016, 20:00
aymanemaysae a écrit:Odonc

et

alors au point (0,0) on a bien un minimum strict .
Un minimum
LOCAL : avec le coup du s^2-rt, tu déduira jamais que du local (ça fait deux fois que je te reprend, mais visiblement, ça rente pas...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 30 Jan 2016, 20:02
par selda6958 » 30 Jan 2016, 20:02
ben314 je n'ai pas compris

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Jan 2016, 20:05
par Ben314 » 30 Jan 2016, 20:05
selda6958 a écrit:ben314 je n'ai pas compris
Tout ce qu'on peut déduire avec des méthode du style différentielle/différentielle seconde, c'est que les points en question sont des minimum/maximum
locaux.
Si on veut montrer que ce sont réellement des minimum/maximum (i.e. globaux), il faut utiliser d'autres arguments.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Jan 2016, 20:07
par Ben314 » 30 Jan 2016, 20:07
Donc par exemple là :
selda6958 a écrit:pour la fonction f(x) c'est un minimum global
aymanemaysae a écrit:Oui, bien vu.
aymanemaysae t'a répondue une connerie vu qu'à priori, tu n'avais rien calculé d'autre que les dérivées partielles (premières et secondes)
Modifié en dernier par
Ben314 le 30 Jan 2016, 20:10, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
selda6958
- Membre Relatif
- Messages: 162
- Enregistré le: 23 Jan 2016, 19:40
-
 par selda6958 » 30 Jan 2016, 20:09
par selda6958 » 30 Jan 2016, 20:09
aymanemaysae

-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 30 Jan 2016, 20:11
par aymanemaysae » 30 Jan 2016, 20:11
Vous avez bien raison M.Ben314: je viens de le voir
ici : un autre site m'a bien eu.
Plus jamais que du Local: c'est bien noté.
Merci.
Edit: je viens de retrouver
ici le Monsieur qui parlait des extremums strict : c'est un site à bannir.
Modifié en dernier par
aymanemaysae le 30 Jan 2016, 20:20, modifié 2 fois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
et
alors au point (0,0) on a bien un minimum strict .