Poincaré direct pour les 1-formes différentielles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
 par robby3 » 11 Avr 2008, 11:15
par robby3 » 11 Avr 2008, 11:15
Bonjour tout le monde,j'ai du mal avec cette exercice...
Soit

une 1-forme fermée dé;)nie sur
un ouvert

de

etoile en 0. On pose
 =\Bigsum_{i=1}^n x_i \Bigint_0^1 \alpha_t(tx) dt)
>Calculer df.
Merci d'avance de votre aide!
mon soucis c'est l'integrale! :triste:
-
mathelot
 par mathelot » 11 Avr 2008, 12:33
par mathelot » 11 Avr 2008, 12:33
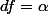
Si

est fermée et U étoilé alors ...
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
 par robby3 » 11 Avr 2008, 18:03
par robby3 » 11 Avr 2008, 18:03
Salut,
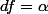
? coment vous faites avec l'integrale?
si

est fermé et

étoilé,on a poincaré donc

est exacte sur U cad il existe une 2-forme sur

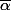
tel que
=\alpha)
non?
 par busard_des_roseaux » 12 Avr 2008, 10:37
par busard_des_roseaux » 12 Avr 2008, 10:37
bjr,

étant fermée et U étoilé,
il existe

telle que
=\alpha(x))
L'application
)
, de

dans

a pour dérivée
g'(t)=dF(tx).x (produit scalaire dans

=nombre dérivé=nb réel)
d'où:
=g(1)-g(0)=F(x)-F(0))
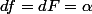
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
 par robby3 » 12 Avr 2008, 22:05
par robby3 » 12 Avr 2008, 22:05
Bonsoir busard_des_roseaux,
je te suis jusque là:
d'où:
=g(1)-g(0)=F(x)-F(0)<br />df = dF = \alpha)
je comprend pas le d'ou? :triste: :hein:
peux tu si tu as le temps expliciter encore plus. :happy2:
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
 par robby3 » 13 Avr 2008, 11:49
par robby3 » 13 Avr 2008, 11:49
Bon,j'essaye de reprendre le fil de la chose.
on veut df.
f
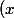 =\Bigsum_{i=1}^n x_i \Bigint_0^1 \alpha_t(tx) dt)
donc
=d(\Bigsum_{i=1}^n x_i \Bigint_0^1 \alpha_t(tx)) dt)
ensuite que fait-on?
la fonction

de départ c'est ce qu'on appelle

par la suite? :mur:
 par busard_des_roseaux » 14 Avr 2008, 09:29
par busard_des_roseaux » 14 Avr 2008, 09:29
bjr,
l'idée , c'est que

se primitive
forme fermée+ ouvert étoilé => forme exacte.
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
 par robby3 » 14 Avr 2008, 13:02
par robby3 » 14 Avr 2008, 13:02
AHHH!!
et on a montré que
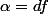
?
ok je crois que j'ai saisi la chose!
Merci bien! :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités