Plan et droite dans l'espace

[Diacht24]

Bonjour,


J'ai du mal à résoudre cet exercice,
pouvez-vous m'aider ? ?

On donne les points ABC et D les sommets de tétraèdre ABCD
A(1,2,0), B(11,2,0), C(17,6,1) et D(9,8,0)
On demande de:
a) Calculer l'aire de la surface totale du tétraèdre ABCD,
b)Le volume du tétraèdre ABCD,
c) Trouver graphiquement le symétrique du tétraèdre ABCD par rapport à l'origine des axes, puis déterminer les coordonnées de ses différents sommets,
d) Ecrire les équations du plan Π passant par le point E(1,8,4) et parallèle à la face ACD du tétraèdre, puis celui du plan ∆ passant par le point F(2,5,3) et perpendiculaire à la face ABD du tétraèdre

[mathelot]

bonsoir,
pour la question (1), on peut calculer l'aire d'un triangle par la formule du déterminant et la vérifier par la formule de Héron
https://fr.wikipedia.org/wiki/Aire_d%27un_triangle

pour la question (2), on peut calculer le volume d'un tétraèdre par la formule du déterminant et la vérifier
par la formule V=(1/3) base x hauteur
https://fr.wikipedia.org/wiki/T%C3%A9tra%C3%A8dre

pour la question (d), comme le plan doit être parallèle à la face ACD, on a comme vecteur normal
au plan où 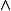est le produit vectoriel de deux vecteurs.

[Diacht24]

Mathelot, je pas compris pour la question (d)
Tu peux me l'expliquer autrement stp

[mathelot]

question (d)
le plan doit être parallèle au plan
En particulier, ces deux plans ont les mêmes vecteurs normaux.
Pour trouver un vecteur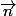 normal à , on construit un vecteur orthogonal à la fois à et non nul;
Pour construire ce vecteur , on forme le produit vectoriel

en effet le vecteur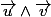 est orthogonal à et

https://fr.wikipedia.org/wiki/Produit_vectoriel