Un peu de topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mounch1810
- Membre Naturel
- Messages: 23
- Enregistré le: 31 Jan 2015, 14:40
-
 par mounch1810 » 01 Fév 2015, 19:35
par mounch1810 » 01 Fév 2015, 19:35
Bonjour à tous,
J'ai vraiment des carences en topo, si vous pouviez m'aider sur cet exercice:
Soit n

1 et soit

un ouvert non vide de

tel que

soit strictement contenu dans

.
On pose:
:=\inf_{y\epsilon\mathbb{R}^n-\Omeg})

,

, où
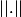
est la norme euclidienne.
1)Montrer que si

et

alors
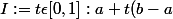\epsilon\mathbb{R}^n-\Omega})
est une partie compacte de

qui contient 0 et ne contient pas 1.
2) En déduire qu'il existe
\epsilon\partial\Omega)
Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Fév 2015, 20:11
par zygomatique » 01 Fév 2015, 20:11
mounch1810 a écrit:Bonjour à tous,
J'ai vraiment des carences en topo, si vous pouviez m'aider sur cet exercice:
Soit n

1 et soit

un ouvert non vide de

tel que

soit strictement contenu dans

.
On pose:
:=\inf_{y\epsilon\mathbb{R}^n-\Omeg})

,

, où
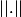
est la norme euclidienne.
1)Montrer que si

et

alors
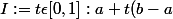\epsilon\mathbb{R}^n-\Omega})
est une partie compacte de

qui contient 0 et ne contient pas 1.
2) En déduire qu'il existe
\epsilon\partial\Omega)
Merci
salut
c'est plutôt
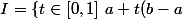 \in \mathbb{R}^n - \Omega \})
et alors que se passe-t-il pour t = 0 ? t = 1 ?
si

est ouvert alors son complémentaire est fermé ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mounch1810
- Membre Naturel
- Messages: 23
- Enregistré le: 31 Jan 2015, 14:40
-
 par mounch1810 » 01 Fév 2015, 20:34
par mounch1810 » 01 Fév 2015, 20:34
zygomatique a écrit:salut
c'est plutôt
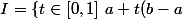 \in \mathbb{R}^n - \Omega \})
et alors que se passe-t-il pour t = 0 ? t = 1 ?
si

est ouvert alors son complémentaire est fermé ...
Oui effectivement I a la forme que tu as mentionnée.
Par contre je ne comprends pas le sens de ta question.
En 0, I={a} et en 1, I={b}, mais d'où vient cette expression, on a au départ


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Fév 2015, 20:38
par zygomatique » 01 Fév 2015, 20:38
non i ne contient que des réels de l'intervalle [0, 1] ...
mais I contient-il 0 ? 1 ?
il faut que u = a + t(b - a) appartienne au complémentaire de Oméga ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mounch1810
- Membre Naturel
- Messages: 23
- Enregistré le: 31 Jan 2015, 14:40
-
 par mounch1810 » 01 Fév 2015, 21:05
par mounch1810 » 01 Fév 2015, 21:05
zygomatique a écrit:non i ne contient que des réels de l'intervalle [0, 1] ...
mais I contient-il 0 ? 1 ?
il faut que u = a + t(b - a) appartienne au complémentaire de Oméga ...
Je pense que

I mais 1 non
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
1 et soit
un ouvert non vide de
tel que
soit strictement contenu dans
.
:=\inf_{y\epsilon\mathbb{R}^n-\Omeg})
,
, où
est la norme euclidienne.
et
alors
est une partie compacte de
qui contient 0 et ne contient pas 1.
est ouvert alors son complémentaire est fermé ...