Un peu d'algèbre
39 messages
- Page 1 sur 2 - 1, 2
Un peu d'algèbre
Bonjour, j'aurai voulu déterminer l'ensemble des homomorphismes de  dans
dans 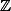 , où
, où  désigne un groupe fini. Déjà, si j'ai bon, on parle de
désigne un groupe fini. Déjà, si j'ai bon, on parle de 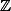 comme étant le groupe
comme étant le groupe ) . Ensuite, j'ai du mal à voir comment on peut éventuellement déterminer de tels morphismes (s'ils existent) :
. Ensuite, j'ai du mal à voir comment on peut éventuellement déterminer de tels morphismes (s'ils existent) :  etant fini et
etant fini et 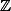 étant d'ordre infini... . Puis j'ai du mal à comprendre, mais si on demande de
étant d'ordre infini... . Puis j'ai du mal à comprendre, mais si on demande de  dans
dans 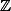 , est-ce que cela signifie que pour tout entier dans
, est-ce que cela signifie que pour tout entier dans  , on demande qu'il ait un antécédent ? (i.e. demande-t-on la surjectivité ?). Des suggestions ?
, on demande qu'il ait un antécédent ? (i.e. demande-t-on la surjectivité ?). Des suggestions ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:salut
soit f un morphisme de (G, +) dans (Z, +)
soit e le neutre de G ... que vaut f(e) ?
soit g un élément de G et -g son "inverse"
f(g) + f(-g) = ?
que vaut f(ng) ?
Alors f(e)=1 et f(g)+f(-g)=0 (Dois-je prouver ces deux égalités ?).
Par contre, j'ai du mal à comprendre quand vous écrivez f(ng), ne voulez vas pas dire plutôt
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Alors f(e)=1 et f(g)+f(-g)=0 (Dois-je prouver ces deux égalités ?)
f(e) = ... ?
et qu'est-ce qui prouve ces deux égalités ?
tu choisis la notation multiplicative mais il semble préférable de choisir la notation additive ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:f(e) = ... ?
et qu'est-ce qui prouve ces deux égalités ?
tu choisis la notation multiplicative mais il semble préférable de choisir la notation additive ....
Pourquoi semble-t-il préférable de choisir un notation additive ?
Est-ce parce que
Adoptons ton idée : posons + cette loi.
En particulier, piur
(j'me suis trompé de neutre : j'avais noté 1 celui de G...).
Pour
Pour
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:ok que pensez-de l'application n --> nf(x) de Z dans Z ?
or G est fini donc .....
Elle est injective puisque pour
Mais pas surjective (je ne vois pas comment le prouver).
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:l'injectivité me suffit ....
sauf que maintenant G est fini donc pour tout g dans G il existe k tel que kg = e
(k est l'ordre de g) ....
Heu, j'ai un peu du mal à voir où l'on veut aller...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Heu, j'ai un peu du mal à voir où l'on veut aller...
oui je te donne des idées et des propriétés un peu en vrac .... pour te laisser arriver à la solution ....
G est fini donc tout élément g de G vérifie kg = e où k est l'ordre de g
donc f(kg) = f(e) = 0
d'autre part f(G) est un groupe .....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:G est fini donc tout élément g de G vérifie kg = e où k est l'ordre de g
donc f(kg) = f(e) = 0
d'autre part f(G) est un groupe .....
f(kg)=kf(g)=0 donc f(g)=0, que que soit g.
Je ne vois pas bien comment ni pourquoi utiliser l'hypothèse f(G) est un groupe. ..
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:G est fini et f(G) est un groupe donc f(G) est un groupe fini ....
oui, je suis d'accord, mais je ne sais pas où on va donc je suis un peu dans le brouillard...
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:ben quels sont les sous-groupes finis de (Z, +) ?
tous les groupes de la forme (nZ,+)
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
zygomatique a écrit:(nZ, +) est fini ?
(voir à 19h24 et 19h49) ....
Non, il n'est pas fini, sauf 0Z={0}
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Si il existe un morphisme de G vers Z alors en fait c'est le morphisme nul i.e. celui qui à tout élément g de G associe 0.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
39 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
