Un peu d'algèbre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Sep 2014, 20:49
par zygomatique » 25 Sep 2014, 20:49
capitaine nuggets a écrit:Si il existe un morphisme de G vers Z alors en fait c'est le morphisme nul i.e. celui qui à tout élément g de G associe 0.
:biere: ..................
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 20:53
par capitaine nuggets » 25 Sep 2014, 20:53
Mais du coup, je ne vois pas pourquoi on a montré que :
- f(e)=0 ;
- f(x)+(-x)=0 ;
- f(nx)=nf(x) ;
- L'application de Z dans Z définie pour tout n par nf(x).
N'aurais-t-on pas pu directement donné l'argument que le seul groupe fini de (Z,+) est {0} pour conclure ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Sep 2014, 20:59
par zygomatique » 25 Sep 2014, 20:59
oui mais comme tu n'en avais pas l'idée j'ai voulu te faire retrouver le fait que f(G) est fini ....puis ensuite conclure .....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 21:07
par capitaine nuggets » 25 Sep 2014, 21:07
zygomatique a écrit:oui mais comme tu n'en avais pas l'idée j'ai voulu te faire retrouver le fait que f(G) est fini ....puis ensuite conclure .....
Ah ok, je pense avoir compris maintenant, merci pour votre aide :+++:
Et que se passerait-il si par exemple
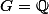
.
Deux questions pour confirmer deux choses :
- Si on a une application f d'un ensemble E dans un ensemble F et que E ou F est un groupe, f vérifie f(xy)=f(x)f(y) alors F ou E est bien un groupe ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 21:29
par capitaine nuggets » 25 Sep 2014, 21:29
zygomatique a écrit:oui mais comme tu n'en avais pas l'idée j'ai voulu te faire retrouver le fait que f(G) est fini ....puis ensuite conclure .....
Ah ok, je pense avoir compris maintenant, merci pour votre aide :+++:
Et que se passerait-il si par exemple
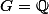
.
Deux questions pour confirmer ce que j'ai pu retenir :
- Si on a une application f d'un ensemble E dans un ensemble F et que E ou F est un groupe, f vérifie f(xy)=f(x)f(y) alors F ou E est bien un groupe ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Sep 2014, 21:29
par zygomatique » 25 Sep 2014, 21:29
pour f : (Q, +) --> (Z, +)
pour tout z entier f(z) = f(z.1) = zf(1)
ensuite qf(p/q) = f(p)
à toi de poursuivre
si f :: E --> F
si E ou F est un groupe on peut sous certaines conditions transporter la structure à E ou à F
remarque :: écrire f(xy) = f(x)f(y) signifie qu'il y a donc une "multiplication" dans E (par définition de l'écriture xy) et dans F (par définition de l'écriture f(x)f(y))
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 21:36
par capitaine nuggets » 25 Sep 2014, 21:36
zygomatique a écrit:pour f : (Q, +) --> (Z, +)
pour tout z entier f(z) = f(z.1) = zf(1)
ensuite qf(p/q) = f(p)
à toi de poursuivre
si f :: E --> F
si E ou F est un groupe on peut sous certaines conditions transporter la structure à E ou à F
remarque :: écrire f(xy) = f(x)f(y) signifie qu'il y a donc une "multiplication" dans E (par définition de l'écriture xy) et dans F (par définition de l'écriture f(x)f(y))
....
Si qf(p/q)=f(p) alors q divise f(p), pour tous p,q. Donc seul le morphisme nul convient là aussi ?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 21:57
par capitaine nuggets » 25 Sep 2014, 21:57
zygomatique a écrit:pour f : (Q, +) --> (Z, +)
pour tout z entier f(z) = f(z.1) = zf(1)
ensuite qf(p/q) = f(p)
à toi de poursuivre
Si qf(p/q)=f(p) alors q divise f(p), pour tous p,q. Donc seul le morphisme nul convient là aussi ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Sep 2014, 22:05
par zygomatique » 25 Sep 2014, 22:05
il semblerait bien ...
si F est un groupe alors dans E on peut poser
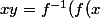f(y)))
qui définit une loi de groupe sur E ....
si E est un groupe on pose f(x)f(y) = f(xy) pour faire de F un groupe
enfin voir et revoir et vérifier .... mais ça me semble aller ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 22:11
par capitaine nuggets » 25 Sep 2014, 22:11
Ok, je regarderais ça.
Du coup, il me vient une question :
On a montrer que si :
- on a un morphisme d'un groupe fini G dans (Z,+) ;
- on a un morphisme de (Q,+) dans (Z,+) ;
alors ce morphisme est nul.
est-ce que (Q,+) est un groupe particulier de G ((Q,+) est-i engendré par un ensemble fini ?) ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 25 Sep 2014, 22:14
par zygomatique » 25 Sep 2014, 22:14
ta question (la dernière phrase) n'est pas claire ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 22:21
par capitaine nuggets » 25 Sep 2014, 22:21
zygomatique a écrit:ta question (la dernière phrase) n'est pas claire ?
Est-ce qu'il existe une ensemble fini

tel que
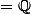
?
J'ai pris un exemple avec
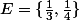
.
Alors on a
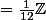
(si je ne dis pas de bêtises...).
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Sep 2014, 22:55
par Doraki » 25 Sep 2014, 22:55
Euh c'est quoi la dimension d'un Z-module ??

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 25 Sep 2014, 23:24
par capitaine nuggets » 25 Sep 2014, 23:24
zygomatique a écrit:Q est un Z-module de dimension infinie sur Z
on ne peut l'engendrer par un ensemble fini
Et comment on peut prouver ce résultat ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 26 Sep 2014, 00:09
par L.A. » 26 Sep 2014, 00:09
Bonsoir,
Si tu considères un nombre fini d'éléments de Q, dont les dénominateurs sont d_1,...,d_n,
alors le sous-groupe, ou sous-Z-module engendré par ces éléments sera contenu dans 1/(d_1...d_n) Z, donc pas égal à Q.
En fait, c'est juste ton exemple avec plus d'éléments...

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Sep 2014, 00:46
par capitaine nuggets » 26 Sep 2014, 00:46
L.A. a écrit:Bonsoir,
Si tu considères un nombre fini d'éléments de Q, dont les dénominateurs sont d_1,...,d_n,
alors le sous-groupe, ou sous-Z-module engendré par ces éléments sera contenu dans 1/(d_1...d_n) Z, donc pas égal à Q.
En fait, c'est juste ton exemple avec plus d'éléments...
Ah oui, en fait c'est tout bête !
Merci beaucoup à vous tous pour vos explications & aides :+++:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 26 Sep 2014, 10:09
par Doraki » 26 Sep 2014, 10:09
Q n'est pas un Z-module libre.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
est un Z module de dimension n sur Z