Un peu d'algèbre linéaire

par **petittaupin** » 28 Juin 2010, 10:24

Bonjour , j'aimerais avoir un peu d'aide sur un exercice qui me pose problème ; voici l'énoncé ;

http://img824.imageshack.us/i/ensea.jpg/

Bien que les 2 premières questions soient triviales ( hem ) , je n'arrive pas à déterminer la base voulue , je ne vois que la base canonique comme réponse ... si quelqu'un pouvait m'éclairer . Merci d'avance

par **girdav** » 28 Juin 2010, 10:56

Bonjour,
je pense que tu as vu que

est un sous-espace vectoriel de

.
Comme les

qui sont dans

sont de degré au plus

,

ne peut être de degré supérieur à ...

par **petittaupin** » 28 Juin 2010, 11:14

à n-3 oui ... Donc la base est simplement (1,X,...,X^(n-3)) ?

par **petittaupin** » 28 Juin 2010, 11:16

Ce n'est même pas ça , vu que l'espace porte sur les P , et non sur les Q , ce serait simplement la base canonique ?....

par **girdav** » 28 Juin 2010, 11:17

Il faut multiplier chacun de ces termes par

.

par **petittaupin** » 28 Juin 2010, 11:19

d'accord , j'ai compris ! merci beaucoup de la réponse . et donc pour finir F est de dimension n+1 ?

par **girdav** » 28 Juin 2010, 11:28

Non, tu as trouvé une base de

qui contient

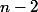
éléments.

par **petittaupin** » 28 Juin 2010, 11:36

comment ça ? on a la base de F , B=((X-b)^3, X(X-b)^3,....., X^(n-3)*(X-b)^3) ,je me rent compte que ca fait une dimension n-3 ... je suis à nouveau perdu ..

par **petittaupin** » 28 Juin 2010, 11:38

oui , n-2 , effectivement . Mais il n'y a pas une contradiction avec le fait que F soit un espace de polynomes de degré n ? la définition ne veut pas que cet espace soit de dimension n+1 ?

par **girdav** » 28 Juin 2010, 11:38

En fait il y a le même nombre d'éléments que dans la base que tu as cité dans le troisième message de la discussion (le fait de multiplier tout le monde par

ne change fort heureusement pas le nombre d'éléments de cette famille). Pour celle-ci, le nombre d'éléments est plus facile à déterminer.

par **girdav** » 28 Juin 2010, 11:39

petittaupin a écrit:oui , n-2 , effectivement . Mais il n'y a pas une contradiction avec le fait que F soit un espace de polynomes de degré n ? la définition ne veut pas que cet espace soit de dimension n+1 ?

Oui, mais

est seulement un sous-espace (propre d'ailleurs).

par **petittaupin** » 28 Juin 2010, 11:44

oui effectivement . je viens de voir aussi que je mélangeais les définitions ... Merci beaucoup pour ces réponses rapides .

par **petittaupin** » 28 Juin 2010, 11:51

j'aurais encore une petite question ... afin de démontrer que Tr(AB)=Tr(BA) , on calcule les éléments diagonaux de AB puis BA , et il faut sommer ses éléments pour se rendre compte de l'égalité , mais il faut utiliser une formule afin de simplifier une somme double ... vous ne vous en rappeleriez pas par hasard ? :id:

par **girdav** » 28 Juin 2010, 11:58

Je m'en souviens (ça ne date pas de si longtemps!). On a

. On permute les deux sommes (ceci est bien licite) puis on tombe bien sur

(quitte à changer les indices).

par **petittaupin** » 28 Juin 2010, 12:00

d'accord , je me demandais si c'était bien licite . Merci encore pour toutes ces réponses !

par **girdav** » 28 Juin 2010, 12:02

D'ailleurs, on peut supposer que

est de taille

et

de

. Le calcul est le même.

par **petittaupin** » 28 Juin 2010, 12:08

hm.. ok :D

Un peu d'algèbre linéaire

un peu d'algèbre linéaire

Qui est en ligne