Petites bizarreries mathématiques

[Rhaegar]

Bonjour à tous ,

J'aimerais savoir où sont les erreurs et une explication dans les égalités suivantes parce que je comprend pas.







Après il y en a une autre un peu pareil.






Encore une. C'est encore avec les puissances.



Et un dernière sur les dérivées



on dérive de chaque coté




Voilà donc si quelqu'un peut m'éclairer ça serait sympa. Merci

[anthony_unac]

Bonsoir,
Il me semble que la propriété n'a de sens que si b et c sont réels d'ou l'erreur

[Rhaegar]

Oui mais en même temps, les nombres que j'utilise sont des réels sous une notation complexe. Donc on aurait une propriété vrai sur des réels mais fausse si on les notes comme des complexes. C'est assez bizarre.

[Ben314]

Salut,
Ben... faut un peu réfléchir dans sa tête...
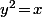
La notation , quelque soit le contexte (groupe, anneau, etc...), ça va évidement désigner UNE des solutions de l'équation et bien sûr, vu que c'est une équation de degré 2, cette solution est très rarement unique et donc la notation est "multivoque" et il faut s'en méfier comme la peste.
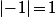
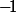
Donc, normalement, on apprend dés le collège que, pour un réel quelconque, n'est pas forcément égal a mais qu'en fait comme le montre justement les deux premiers exemples que tu donne qui est celui de qui est égal à et pas à et dans la même veine, on est aussi sensé y apprendre que, justement, 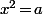n'est pas équivalent à avec les notation du collège) ce qui traduit bien le coté "multivoque" du bidule.

Et, effectivement, lorsque l'on voit ensuite des formules du type général , on met bien en garde les élèves que, comme toute formules mathématique qui se respecte, il faut faire précéder cette formules d'un certain nombre de quantificateurs en donnant la "portée" et que, en l'occurrence, les quantificateurs sont :
Ou bien .
Ou bien .
Ou bien .
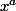
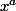
L'existence des trois formules provenant des 3 définition de ce que représente selon que a est entier naturel, entier relatif ou réel quelconque (dans le dernier cas, est égal à et n'a de sens que pour réel strictement positif)

[Ben314]

on dérive de chaque coté...

Et sinon, ça, c'est évidement dénué de sens dés le départ : quand on défini la notion de dérivée, on te parle de limite lorsque h tend vers 0 de (f(x+h)-f(x))/h et on t'explique (normalement) qu'évidement, pour que ça ait du sens, il faut que non seulement f(x) existe, mais bien sûr aussi que f(x+h) existe pour les "petites" valeurs de h.
Or, lorsque tu écrit qu'on additionne x fois quelque chose, ça signifie bien évidement que x est un entier et, tout aussi clairement, si h est petit, ben x+h ne sera pas un entier donc ça aura aucun sens de parler d'une somme de x+h termes donc aucun sens de parler de f(x+h) et donc de parler de la dérivée d'un truc pareil.
Bref, c'est tout aussi crétin que de parler de la tangente à une soit disant courbe qui ne serait en fait constituée que d'un seul et unique point : comment veut tu que la notion de tangente ait du sens dans ce cas là ?

Et pour finir, même si on tentait de donner du sens à un truc pareil, par exemple en considérant que ça a du sens de parle d'une addition de 3,25 termes, ça ne marcherais pas quand même vu que le théorème qui dit que, si f et g sont dérivable sur I alors f+g l'est aussi avec (f+g)'=f'+g', si tu cherche à le généraliser, tu va montrer que ça continuer à marcher pour une somme finie et évidement entière de fonction et, si tu cherche à le généraliser encore plus à travers une notion de "somme pas entière" de fonctions, ça ne marchera que si le nombre d'élément de la somme ne dépend pas de x vu que ce que tu va obtenir, ben ça sera en fait la même chose que le théorème qui dit que la dérivée de x->a.x est x->a et qui évidement stipule bien que ce n'est valable que si a est une constante et pas un truc qui dépend de x (par exemple, la dérivée de x->sin(x).x=a.x, avec a=sin(x) ben c'est absolument pas x->a c'est à dire x->sin(x))

[Rhaegar]

Ok je comprend mieux d'où viennent les incohérences. Je me doutais bien que la notation avait plusieurs sens. Mais du coup, le fait de dire que est une sorte de convention car on pourrait également dire .

Je ne connaissais pas les définitions exactes de donc difficile pour moi de savoir où ça n'allait pas. On m'a surement enseigné au collège/Lycée ces définitions mais malheureusement, je ne peux pas retenir absolument tous ce qu'on m'apprend.

Et pour la dérivée, je n'avais pas pensé au fait que la somme ayant un nombre variable de termes implique que la formule ne marche pas. C'est vrai que maintenant ça ma parait évident.

Merci pour les explications qui ont été très précises

[Ben314]

Mais du coup, le fait de dire que est une sorte de convention car on pourrait également dire .

Tout à fait : c'est par convention qu'on a choisi de dire que ce qu'on appellerais LA racine carré d'un réel positif A, c'est, parmi les deux solutions de l'équation X²=A celle des deux qui est positive. C'est évidement bien plus pratique que d'être obligé d'écrire à chaque fois en Français "soit bidule une des deux solutions de l'équation X²=A", mais... c'est un peu piège à con... vu ce coté arbitraire d'avoir privilégié une des deux solutions par rapport à l'autre.

[zygomatique]

enfin ça permet une cohérence car sinon on n'aurait plus les propriétés que possèdent la racine carrée

car en prenant la racine négative alors on arrive une contradiction avec la racine d'un produit et la règle des signes :







donc

et c'est exactement ce que tu fais implicitement dans tes ""démonstrations"

[Ben314]

car en prenant la racine négative alors on arrive une contradiction avec la racine d'un produit et la règle des signes :

Oui et non : perso, j'aurais plutôt exprimé ça en disant que si on avait pris comme convention de prendre la racine négative alors "la règle du produit" ne serait évidement plus mais qui est un peu moins "mnémotechnique" et un peu plus chiante à mémoriser, surtout pour un produit de n termes où on aurait un (-1)^(n-1) devant les racines. Mais bon, les "règles" en maths, elle ne sont pas toutes super mnémotechnique non plus, par exemple si c'était égal à ça serait évidement plus mnémotechnique. . .

[zygomatique]

oui effectivement c'est plutôt: on change les règles de calcul !!!

et c'est même plutôt un (-1)^{n - 1} encore plus c... à mémoriser !!!

[Ben314]

Oui : je rectifie.

Sinon, en étant honnête, il faut quand même reconnaitre que, vu qu'on ne prend que des racines de réels positifs, c'est quand même infiniment plus naturel de conserver la solution positive de l'équation que la négative de façon à avoir une fonction de R+ dans R+ (et qui est un morphisme de groupe de (R+*,x) dans lui même. Donc le bon sens commande soit de prendre cette solution là, soit de n'en prendre aucune et de ne pas définir de fonction racine carré et d'en rester (comme on le fait dans C) à écrire "une des racines carrés de ...".

[Rhaegar]

Okok merci tout le monde.

[alphamethyste]

salut
pour ne pas se retrouver avec des problèmes il suffit d'utiliser le langage des ensembles
il suffit de dire que l 'on pose quatre relations: deux fonctionnelles et qui sont des applications et qui s'écrivent de manière identiques et deux non fonctionnelles et qui s'écrivent de manière identiques
-la première c'est une application en l'écrivant pour l'application
telle que
-la deuxième c'est une relation non fonctionnelle en l'écrivant pour la relation non fonctionnelle telle que

Attention ainsi définie cette racine peut être complexe
-la troisième c'est une application en l'écrivant pour l'application telle que
lorsque alors
lorsque alors
-la quatrième c'est une relation non fonctionnelle en l'écrivant pour la relation non fonctionnelle telle que

[Rhaegar]

Ducoup alphamethyste, si j'ai bien compris :
dans la deuxième définition, dire que avec , c'est désigné toute les solutions telles que
Et la quatrième définition, c'est la même sauf que maintenant

Par contre la troisième j'ai pas compris.

[Ben314]

Perso, plutôt que tout ce charabia grandiloquent, il me semble de loin préférable d'utiliser ce que tout le monde utilise, c'est à dire... du Français... : Soit y une (des) racines carrés de x.
Que ce soit dans le cas des complexes où on parle du groupe des racines n-ième de l'unité et de l'ensemble des racines n-ièmes d'un complexe donné ou dans le cas des corps fini où on emploie le même vocabulaire, je ne voit aucun intérêt à utiliser quelconque symbolisme (pourri) pour parler du bidule.
Bref, à mon sens, ce genre de verbiage, ça rentre direct dans la catégorie "pourquoi faire simple quand on peut faire compliqué" au moins jusqu'au moment où on voit la notion de revêtement universel d'un espace topologique (en l'occurrence C*) où ça peut être pertinent de parler des "fibres" au dessus d'un point.

Et quand je vois des horreur du type "relation non fonctionnelles" avec écrit à coté en toute lettres du c^(1/2)=b avec le symbole usuel = pour désigner un truc qui ne peut pas être une égalité au sens mathématique vu que b est un réel alors que c^(1/2) n'en est pas un, ben ça me conforte sacrément dans mon opinion consitant à penser qu'à part inciter à écrire des énormités de ce type, je vois pas l'intérêt.

[Ben314]

dans la deuxième définition, dire que avec , c'est désigné toute les solutions telles que

Sauf que ce type de connerie, c'est en contradiction profonde avec le sens même du symbole = qui doit être réflexif, c'est à dire que a=b et b=c doit impliquer a=c alors que là, et n'implique pas

Si tu veut poser une définition de ce type, alors va désigner l'ensemble des solutions de l'équation et ce que tu écrira, c'est que et ce qui, on ne peut plus clairement, n'implique pas .
Bref, pour parler de ça correctement, le symbolisme, on l'a déjà (et on l'utilise on ne peut plus souvent) : c'est d'associer à une équation l'ensemble de ces solutions.

En résumé, tu oublie tout de suite ce style de connerie, y compris la notion d'application "racine carré" dans C qui est de nouveau on ne peut plus piège à con. Tu verra (plus tard) ce qu'on appelle des "détermination" de la fonction argument sur C qui permettent de définir des fonction racines carrées. Sauf que pour utiliser sans risque ce genre d'outil, il faut avoir parfaitement compris de quoi il retourne (En math, comme ailleurs, ne jamais mettre la charrue avant les bœufs)

[alphamethyste]

f(a)=b et f(a)=c ne signifie pas b=c si on précise que la relation f n'est pas fonctionnelle
donc il est tolérable d'écrire f(a)=b si on dit que f n'est pas fonctionnelle
et si on dit que f(a)=b sans préciser cela alors oui ça serai une faute mais ici je l'ai dit

pour la 3) c'est une convention d'écriture qui si elle est posée reste valable
et si on dit cela sans le préciser alors oui cela serai une faute mais ici j'ai dit que je le posais

[Lostounet]

Perso, plutôt que tout ce charabia grandiloquent,
.

Absolument marre de tout ce volume de conneries que tu débites systématiquement, Alphaméthyste depuis ton inscription. D'ailleurs il me semble t'avoir déjà banni, mais qu'importe, je le refais.

[Rhaegar]

Ecrire , ça pose pas de problème, c'est multiplié par lui-même. Par contre, écrire , j'ai l'impression qu'on ne peut pas le faire à moins de poser une convention. Sinon on a plusieurs résultats différents ce qui n'est pas possible ducoup.