Petite théorie des groupes

[simplet]

:id: questions rapides:

_Soit G un groupe d'ordre 8 et Z(G) son centre.
On a préalablement montré qu'il y avait un élément a de G d'odre 4, et que H= était distingué.
Pourquoi diable le centre ne peut-il pas alors etre d'ordre 1 ??

_Autre fast question.
Dans le corps Complexe, où i et j sont avec leur définition usuelle;
pourquoi ji(j-1)=i-1 où a-1 est l'inverse de a pour la loi multiplicative dans le corps complexe.

merci

[quinto]

:id: questions rapides:

_Soit G un groupe d'ordre 8 et Z(G) son centre.
On a préalablement montré qu'il y avait un élément a de G d'odre 4, et que H= était distingué.
Pourquoi diable le centre ne peut-il pas alors etre d'ordre 1 ??

Tu as un p-groupe. (ie groupe d'ordre p^k)
Un p-groupe n'a jamais de centre trivial.

[Galt]

Ton groupe est le groupe des isométries du carré (composé de la rotation r d'angle et de ses trois puissances, et des 4 symétries par rapport aux médianes et aux diagonales). Son centre est composé de l'identité et de 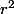. Je n'ai pas de preuve évidente pour l'instant.
Ton 2ème problème me semble faux (la multiplication dans C est commutative, on trouve i)

[quinto]

Oui, ou sinon on fait comme je dis, c'est à dire que l'on a un p groupe, et donc son centre ne peut pas etre trivial, sauf si le groupe lui même l'est.