Petite question sur les réels
30 messages
- Page 1 sur 2 - 1, 2
Petite question sur les réels
Petite question
Quand on se donne un ensemble de nombres réels finis, par exemple A = {0,5,9,racine de 10}.
Quel théorème permet d'affirmer qu'il y en a un qui est nécessairement le plus grand. Bien sûr c'est hyper intuitif.
L'axiome de la borne supérieure ? Si c'est celui-là alors comment savoir si c'est majoré quand on ne connait pas les nombres ? Par exemple si B est un ensemble de 4 nombres réels ?
Quand on se donne un ensemble de nombres réels finis, par exemple A = {0,5,9,racine de 10}.
Quel théorème permet d'affirmer qu'il y en a un qui est nécessairement le plus grand. Bien sûr c'est hyper intuitif.
L'axiome de la borne supérieure ? Si c'est celui-là alors comment savoir si c'est majoré quand on ne connait pas les nombres ? Par exemple si B est un ensemble de 4 nombres réels ?
Re: Petite question sur les réels
Bonjour,
Le théorème est "IR est un corps totalement ordonné ; plus précisément, c'est l'unique corps à isomorphisme près, totalement ordonné, archimédien et possédant la propriété de la borne supérieure".
Sinon, pour revenir sur une vision plus "basique", on peut définir la relation d'ordre sur IR par

Et dans la construction de IR (par couches successives : puis
puis 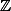 puis
puis 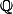 puis
puis  ) on obtient aisément que
) on obtient aisément que  et
et  ce qui montre que la relation d'ordre est bien une relation d'ordre est total.
ce qui montre que la relation d'ordre est bien une relation d'ordre est total.
Le théorème est "IR est un corps totalement ordonné ; plus précisément, c'est l'unique corps à isomorphisme près, totalement ordonné, archimédien et possédant la propriété de la borne supérieure".
Sinon, pour revenir sur une vision plus "basique", on peut définir la relation d'ordre sur IR par
Et dans la construction de IR (par couches successives :
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Petite question sur les réels
Bonjour hdci
Merci pour ta réponse complète !
Je prends un ensemble de nombres réels finis.
Ce n'est évidemment pas vide. Mais pour appliquer l'axiome de la borne supérieure, il faut un argument qui permet de montrer que cet ensemble est majoré.
Avec Archimède ?
Merci pour ta réponse complète !
Je prends un ensemble de nombres réels finis.
Ce n'est évidemment pas vide. Mais pour appliquer l'axiome de la borne supérieure, il faut un argument qui permet de montrer que cet ensemble est majoré.
Avec Archimède ?
Re: Petite question sur les réels
La propriété de la borne supérieure, c'est "toute partie majorée admet une borne supérieure".
Quand la partie de IR est finie non vide, elle est majorée, elle admet même un plus grand élément (qui du coup est la borne supérieure). Cela se démontre facilement par récurrence (faites l'exercice) et du coup la propriété de la borne supérieure n'intervient pas (puisqu'on parle du plus grand élément).
D'ailleurs,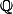 n'a pas la propriété de la borne supérieure, pourtant toute partie finie non vide de rationnels admet un plus grand élément (avec la même démonstration).
n'a pas la propriété de la borne supérieure, pourtant toute partie finie non vide de rationnels admet un plus grand élément (avec la même démonstration).
L'est la totalité de l'ordre et la caractéristique finie qui est utilisée. Généralisez cela à tout ensemble totalement ordonné et une partie finie non vide de cet ensemble.
Essayez de trouver un contre-exemple dans un ensemble non totalement ordonné.
Quand la partie de IR est finie non vide, elle est majorée, elle admet même un plus grand élément (qui du coup est la borne supérieure). Cela se démontre facilement par récurrence (faites l'exercice) et du coup la propriété de la borne supérieure n'intervient pas (puisqu'on parle du plus grand élément).
D'ailleurs,
L'est la totalité de l'ordre et la caractéristique finie qui est utilisée. Généralisez cela à tout ensemble totalement ordonné et une partie finie non vide de cet ensemble.
Essayez de trouver un contre-exemple dans un ensemble non totalement ordonné.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Petite question sur les réels
Je comprends mieux.
Je me lance.
Soit E une partie non vide de R comportant n éléments.
On a E = {a1, ..., an}.
On va montrer qu'elle est majoré quel que soit l'entier naturel n.
Quand n = 1, l'ensemble {a1} est majorée par a1.
Si n est un entier tel que {a1, ..., an} est majoré, alors ...
J'ai pensé à former la réunion {a1, ..., an} u {a(n+1)}. Le premier ensemble est majoré par HR. Je pense qu'en réfléchissant encore un peu, je parviendrai à finir.
Qu'en penses-tu ?
Je me lance.
Soit E une partie non vide de R comportant n éléments.
On a E = {a1, ..., an}.
On va montrer qu'elle est majoré quel que soit l'entier naturel n.
Quand n = 1, l'ensemble {a1} est majorée par a1.
Si n est un entier tel que {a1, ..., an} est majoré, alors ...
J'ai pensé à former la réunion {a1, ..., an} u {a(n+1)}. Le premier ensemble est majoré par HR. Je pense qu'en réfléchissant encore un peu, je parviendrai à finir.
Qu'en penses-tu ?
Re: Petite question sur les réels
C'st le bon départ.
Maintenant que {a1,... an} possède un plus grand élément, que l'ensemble est totalement ordonné, que peut-on dire de a(n+1) ?
Maintenant que {a1,... an} possède un plus grand élément, que l'ensemble est totalement ordonné, que peut-on dire de a(n+1) ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Petite question sur les réels
La totalité de l'ordre va faire que le plus grand élément de l'ensemble {a1,... an} est comparable avec a(n+1). Mais on ne sait pas si c'est lui le plus grand au final.
Si c'est le plus grand élément de l'ensemble {a1,... an} (je le note G), alors a(n+1) <= G.
Sinon c'est G <= a(n+1).
Dans les deux cas, l'ensemble {a1,... an} u {a(n+1)} = {a1,... an,a(n+1)} admet un plus grand élément.
Si c'est le plus grand élément de l'ensemble {a1,... an} (je le note G), alors a(n+1) <= G.
Sinon c'est G <= a(n+1).
Dans les deux cas, l'ensemble {a1,... an} u {a(n+1)} = {a1,... an,a(n+1)} admet un plus grand élément.
Re: Petite question sur les réels
C'est cela, il n'y a plus qu'à terminer la récurrence avec la bonne conclusion (formuler "initialisation + hérédité").
Contre-exemple dans un ensemble qui n'est pas totalement ordonné ?
Contre-exemple dans un ensemble qui n'est pas totalement ordonné ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Petite question sur les réels
Je viens de me rendre compte que je vous tutoyé alors que vous m'avait vouvoyé  . Excusez-moi.
. Excusez-moi.
Je n'ai pas compris votre question. Quel contre-exemple exactement que je dois trouver ?
Je n'ai pas compris votre question. Quel contre-exemple exactement que je dois trouver ?
Re: Petite question sur les réels
Un ensemble muni d'une relation d'ordre, non totale, et une partie finie de l'ensemble qui n'admet pas de plus grand élément
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Petite question sur les réels
Ah ok.
Je prends l'ensemble E définie par E = {2,3,4}.
Je note P(E) l'ensemble de ses parties.
Je prends une partie de P(E), par exemple {{2},{3}}.
On a ni {2} c {3} ni l'inverse.
Je prends l'ensemble E définie par E = {2,3,4}.
Je note P(E) l'ensemble de ses parties.
Je prends une partie de P(E), par exemple {{2},{3}}.
On a ni {2} c {3} ni l'inverse.
Re: Petite question sur les réels
Si ce n'est pas trop demandé je voulais revenir à votre premier message. Je cite :
Le théorème est "IR est un corps totalement ordonné ; plus précisément, c'est l'unique corps à isomorphisme près, totalement ordonné, archimédien et possédant la propriété de la borne supérieure".
Sinon, pour revenir sur une vision plus "basique"...
Si j'ai bien compris, il existe au moins deux versions possibles pour présenter les axiomes de R ?
La première version permet-elle de justifier que la somme de deux réels positifs est positive ?
Le théorème est "IR est un corps totalement ordonné ; plus précisément, c'est l'unique corps à isomorphisme près, totalement ordonné, archimédien et possédant la propriété de la borne supérieure".
Sinon, pour revenir sur une vision plus "basique"...
Si j'ai bien compris, il existe au moins deux versions possibles pour présenter les axiomes de R ?
La première version permet-elle de justifier que la somme de deux réels positifs est positive ?
Re: Petite question sur les réels
Bonjour,
Quelle est cette première version ?
Les axiomes de corps ordonné comprennent le fait que la somme de deux éléments positifs est positive.
Quelle est cette première version ?
Les axiomes de corps ordonné comprennent le fait que la somme de deux éléments positifs est positive.
Re: Petite question sur les réels
Bonjour GaBuZoMeu,
D'accord.
Je pensais qu'il y avait une autre axiomatisation possible (c'est ce que j'ai appelé version) où on pouvait démontrer que la somme de deux réels positifs est un réel positif.
D'accord.
Je pensais qu'il y avait une autre axiomatisation possible (c'est ce que j'ai appelé version) où on pouvait démontrer que la somme de deux réels positifs est un réel positif.
Re: Petite question sur les réels
Je suis en train de lire ceci :
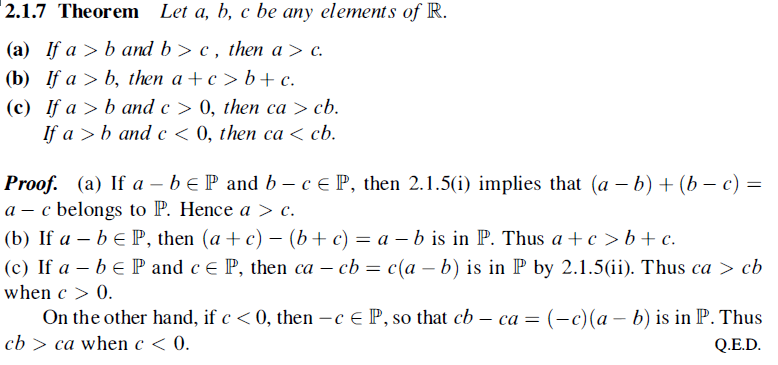
Même si je ne montre pas tout, on est bien ici avec les axiomes de corps ordonné.
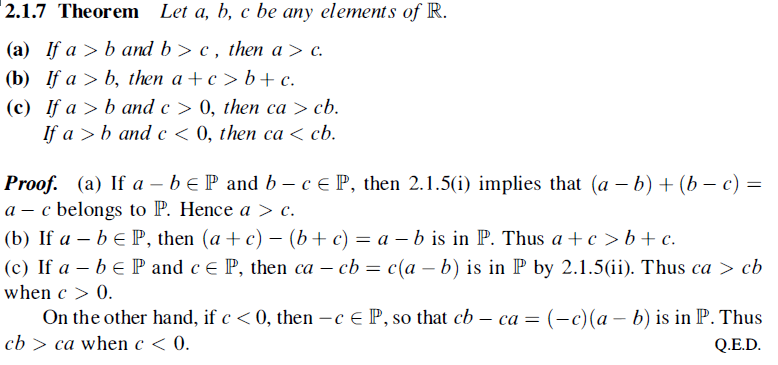
Même si je ne montre pas tout, on est bien ici avec les axiomes de corps ordonné.
Re: Petite question sur les réels
D'accord.
Je vais attendre hdci.
Dans sa première réponse, il laissait entendre qu'il y avait plusieurs moyens d'axiomatiser R. Plus précisément, au niveau de l'ordre et de la positivité.
Je vais attendre hdci.
Dans sa première réponse, il laissait entendre qu'il y avait plusieurs moyens d'axiomatiser R. Plus précisément, au niveau de l'ordre et de la positivité.
Re: Petite question sur les réels
La notion de corps ordonné est bien claire, pas de problème. Et dans un corps ordonné la somme de deux éléments positifs est positive. C'est un axiome, ou ça se démontre directement à partir des axiomes (les axiomes peuvent différer, mais c'est toujours la même théorie).
Quand on construit (par les suites de Cauchy, ou par les coupures de Dedekind) on démontre que
(par les suites de Cauchy, ou par les coupures de Dedekind) on démontre que  est un corps ordonné.
est un corps ordonné.
Quand on construit
Re: Petite question sur les réels
Je ne sais pas si je laissais entendre qu'il y avait plusieurs moyen d'axiomatiser IR, personnellement je n'en connais qu'un seul, à partir de Q les rationnels (mais avec deux moyens, les coupures de Dedekind ou les suites de Cauchy).
L'axiomatisation de IN jusqu'à Q est assez triviale, mais on peut axiomatiser IN de plusieurs façons : à la façon de Peano (non vide car contient 0, existence d'une injection de IN dans IN* appelée "successeur" et le principe de récurrence), ou bien avec les axiomes de l'ordre (non vide, bien ordonné c-à-d toute partie non vide admet un plus petit élément, toute partie majorée admet un plus grand élément et IN lui-même n'est pas majoré), ou bien encore dans la théorie ZFC avec l'axiome de l'infini.
Ces différentes façons sont équivalentes (avec Peano on définit un ordre total, avec les axiomes de l'ordre on démontre le principe de récurrence, et l'axiome de l'infini induit le principe de récurrence), dans les trois cas on obtient un ordre total.
On définit ensuite classiquement la relation d'équivalence que j'appelle "goalaverage" : (n,p) relié à (n',p') ssi n+p'=n'+p, on injecte IN dans les classes d'équivalence et cet ensemble s'appelle Z, la relation d'ordre y est induite et il y a ainsi les positifs et les négatifs.
Pour Q on définit dans Z la relation d'équivalence (n,p) relié à (n',p') ssi np'=n'p et on procède de même, les classes d'équivalence, l'injection de Z, le prolongement de la relation d'ordre.
Pour IR avec les suites de Cauchy, relation d'équivalence sur les suites (la différence est de limite nulle) et on peut à nouveau y injecter Q et prolonger la relation d'ordre. Si on procède par coupure de Dedekind, IR est en fait l'ensemble des sections finissantes de Q et on a également l'injection et le prolongement de la relation d'ordre.
Avec ce mécanisme, on démontre que IR est totalement ordonné, archimédien et possède la propriété de la borne supérieure (avec comme définition de "corps totalement ordonné" la compatibilité de l'ordre avec la multiplication, ce qui n'est pas le cas dans C par exemple). On démontre ensuite qu'un corps ayant ces mêmes propriétés est isomorphes à IR.
L'axiomatisation de IN jusqu'à Q est assez triviale, mais on peut axiomatiser IN de plusieurs façons : à la façon de Peano (non vide car contient 0, existence d'une injection de IN dans IN* appelée "successeur" et le principe de récurrence), ou bien avec les axiomes de l'ordre (non vide, bien ordonné c-à-d toute partie non vide admet un plus petit élément, toute partie majorée admet un plus grand élément et IN lui-même n'est pas majoré), ou bien encore dans la théorie ZFC avec l'axiome de l'infini.
Ces différentes façons sont équivalentes (avec Peano on définit un ordre total, avec les axiomes de l'ordre on démontre le principe de récurrence, et l'axiome de l'infini induit le principe de récurrence), dans les trois cas on obtient un ordre total.
On définit ensuite classiquement la relation d'équivalence que j'appelle "goalaverage" : (n,p) relié à (n',p') ssi n+p'=n'+p, on injecte IN dans les classes d'équivalence et cet ensemble s'appelle Z, la relation d'ordre y est induite et il y a ainsi les positifs et les négatifs.
Pour Q on définit dans Z la relation d'équivalence (n,p) relié à (n',p') ssi np'=n'p et on procède de même, les classes d'équivalence, l'injection de Z, le prolongement de la relation d'ordre.
Pour IR avec les suites de Cauchy, relation d'équivalence sur les suites (la différence est de limite nulle) et on peut à nouveau y injecter Q et prolonger la relation d'ordre. Si on procède par coupure de Dedekind, IR est en fait l'ensemble des sections finissantes de Q et on a également l'injection et le prolongement de la relation d'ordre.
Avec ce mécanisme, on démontre que IR est totalement ordonné, archimédien et possède la propriété de la borne supérieure (avec comme définition de "corps totalement ordonné" la compatibilité de l'ordre avec la multiplication, ce qui n'est pas le cas dans C par exemple). On démontre ensuite qu'un corps ayant ces mêmes propriétés est isomorphes à IR.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

