Petite question matrice diagonale.

[Kimou]

Bonjour à tous,

j'ai un examen demain et en révisant je me suis posé une question:
Si je sais que A est diagonalisable, disons que son polynôme caractéristique comporte des valeurs propres de multiplicités > 1 ; peut on toujours affirmer que le polynôme minimal est le même que le polynôme caractéristque avec toute les puissances misent à 1?? Est-ce cela qu'on appelle "racine simple"?

Je ne sais pas si je me suis très bien exprimé mais si vous ne comprenez pas je ferais un exemple concret (c'est pour éviter d'utiliser latex^^).

Merci bien

[Ben314]

Bonsoir,
C'est effectivement une condition nécéssaire et suffisante pour que A soit diagonalisable (le fait que le poly min. de A soit un produit de (X-ai)^1 avec les ai distincts). On peut effectivement énoncer ce résultat en disant que les valeurs propres (i.e. les ai) doivent être racines simples du polynôme minimal.

Faire aussi attention au fait que dans un corps non algébriquement clos (par exemple ) une obstruction à la diagonalisation peut être le fait que le polynôme minimal n'est pas scindé (i.e. ne se décompose pas en polynômes du premier degrés)
Par exemple a pour poly. char. (et poly. min.) donc n'est pas diagonalisable sur mais l'est sur 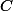car

Bonne chance pour demain...

[Kimou]

Bonsoir,
C'est effectivement une condition nécéssaire et suffisante pour que A soit diagonalisable (le fait que le poly min. de A soit un produit de (X-ai)^1 avec les ai distincts)

merci bien !