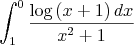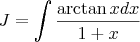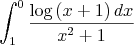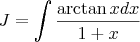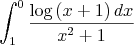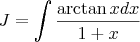Petite problème pour trouver une intégration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mekkadra
- Membre Naturel
- Messages: 24
- Enregistré le: 22 Déc 2011, 18:13
-
 par Mekkadra » 06 Avr 2012, 18:53
par Mekkadra » 06 Avr 2012, 18:53
[CENTER]Bonsoir les jeunes
S'il vous plaît m'aider à trouver cette intégration
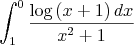
a laid d'un changment de variable défini par
x=1-t/1+tAlors que je peux trouver l'intégration
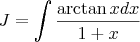
Merci d'avance .[/CENTER]

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Avr 2012, 19:34
par chan79 » 06 Avr 2012, 19:34
Mekkadra a écrit:[CENTER]Bonsoir les jeunes
S'il vous plaît m'aider à trouver cette intégration
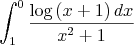
a laid d'un changment de variable défini par
x=1-t/1+tAlors que je peux trouver l'intégration
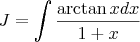
Merci d'avance .[/CENTER]
bonsoir
calcule dx en fonction de dt et mets ton résultat
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 08 Avr 2012, 18:51
par ev85 » 08 Avr 2012, 18:51
Mekkadra a écrit:[CENTER]Bonsoir les jeunes
S'il vous plaît m'aider à trouver cette intégration
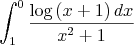
a laid d'un changment de variable défini par
x=1-t/1+tAlors que je peux trouver l'intégration
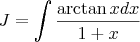
Merci d'avance .[/CENTER]
Je savais que je l'avais quelque part ! Bon il y a des signes à remettre d'aplomb, mais tout y est :
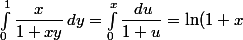)
.
}{1+x^2} \,d x = \int_0^1 \dfrac{\,d x}{1+x^2} \int_{0}^{1} \dfrac{x}{1+xy}\,d y = \iint_{[0,1]^2} \dfrac{x\,d x\,d y}{(1+x^2)(1+xy)})
D'après la propriété de Fubini. Maintenant on a aussi bien sûr, par symétrie~:
(1+xy)})
, donc
(1+xy)} + \dfrac{x}{(1+x^2)(1+xy)}\right) \,d x\,d y = \dfrac12 \iint_{[0,1]^2}\dfrac{(x+y)\,d x\,d y}{(1+x^2)(1+y^2)} = \iint_{[0,1]^2}\dfrac{x\,d x\,d y}{(1+x^2)(1+y^2)})
,
de nouveau grâce à la symétrie. Donc
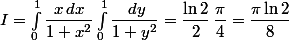
.
Bon, avec le changement de variable, c'est rigolo aussi, je dois l'avouer.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 111 invités