Petite probabilité

par **popo_51** » 10 Sep 2006, 10:36

coucou ,voila j'ai un petit probleme de probabilité ,l'enoncé est quelle est la probabilite quau moins 2 etudiants de la classe de BCPST (jai pris une variable m)possedent le mm jour d'anniversaire (on ne tient pas compte de l'annee)
il faut egalement emettre des hyp qui simposent pr modeliser simplemnt et efficacemt la situation
jai emis les hypothese que les naissances se repartissent uniformement tt au long de lannee
jai egalement reformé le pb ac des boules/jai 365 boules differentes ,je tire m fois ac remise
Quelle est la proba davoir au moins 2 fois la mm boule?
jai trouver le nombres de tirages possibles:(365)^m
je me suis dis que P(au moins 2fois la mm boule)=1-P(avoir aucune boule identique )

ms apres je bloque pouvez vous me donner des pistes de reponses ,des idees

merci davance

par **Clembou** » 10 Sep 2006, 11:08

Bonjour,

Fais attention à l'orthographe et éviter le langage SMS :lol4:

popo_51 a écrit:jai 365 boules differentes ,je tire m fois ac remise

Donc la formule qui permet d'avoir cette probabilité est :

par **Flodelarab** » 10 Sep 2006, 17:11

Clembou, arrete definitivement le dénombrement ....

par **Clembou** » 10 Sep 2006, 17:15

Flodelarab a écrit:Clembou, arrete definitivement le dénombrement ....

Toi qui est si malin, explique ton raisonnement

par **Flodelarab** » 10 Sep 2006, 17:18

Clembou a écrit:Toi qui est si malin, explique ton raisonnement

1) une probabilité est un nombre entre 0 et 1.
2) un arrangement s'utilise quand l'ordre intervient .... mettre en ordre 1 élément, c soit très dur soit très facile
3) un arrangement est sans répétition. Alors qu'on te parle de remise.

Quelque soit la solution du probleme, ta modélisation est archi fausse

par **BancH** » 10 Sep 2006, 17:35

Si on prend l'événement inverse, le premier étudiant à le choix entre

dates, le second entre

, le troisième entre

... le m-ième entre

On a alors

et on divise par

par **Flodelarab** » 10 Sep 2006, 17:36

popo_51 a écrit:coucou ,voila j'ai un petit probleme de probabilité ,l'enoncé est quelle est la probabilite quau moins 2 etudiants de la classe de BCPST (jai pris une variable m)possedent le mm jour d'anniversaire (on ne tient pas compte de l'annee)
il faut egalement emettre des hyp qui simposent pr modeliser simplemnt et efficacemt la situation
jai emis les hypothese que les naissances se repartissent uniformement tt au long de lannee
jai egalement reformé le pb ac des boules/jai 365 boules differentes ,je tire m fois ac remise
Quelle est la proba davoir au moins 2 fois la mm boule?
jai trouver le nombres de tirages possibles:(365)^m
je me suis dis que P(au moins 2fois la mm boule)=1-P(avoir aucune boule identique )

ms apres je bloque pouvez vous me donner des pistes de reponses ,des idees

merci davance

Je pense que tu as tout trouvé.

les m étudiants doivent prendre m dates différentes (tirage sans répétition) parmi les 365, indépendemment de l'ordre (on se moque de savoir si Paul est né le 3 et Jaques le 4 ou l'inverse).
C'est donc une combinaison.

d'ou la probablité:

Commentons ce résultat:
S'il y a 366 élèves dans la classe, la formule n'est pas appliquable mais on est sur que 2 personnes sont nés le même jour.

par **Flodelarab** » 10 Sep 2006, 17:37

BancH a écrit:Si on prend l'événement inverse, le premier étudiant à le choix entre dates, le second entre , le troisième entre ... le m-ième entre

On a alors

et on divise par

tu as malgré toi fais intervenir l'ordre!!! Dans ton tirage. Faut diviser encore

:++:

par **BancH** » 10 Sep 2006, 17:38

Ah oui tu as raison...

par **BancH** » 10 Sep 2006, 17:49

Enfin... tu es sûr que l'ordre est important ?

Parce que là si y a deux gars on a:

Ca donne

...

par **BancH** » 10 Sep 2006, 17:53

Enfin... tu es sûr que l'ordre est important ?

Parce que là si y a deux gars on a:

Ca donne

...

par **Flodelarab** » 10 Sep 2006, 22:57

Ce probleme me gave.

L'ordre interviendrait donc bien.

Mais je ne suis toujours pas convaincu.
Je ne trouve pas a quel moment ...

I'll be back!

par **BancH** » 11 Sep 2006, 05:43

C'est clair, c'est louche.

Je pense que c'est parce qu'on est trop habitué à des énoncés du style: quelle est la probabilité pour que deux personnes aient comme jour de naissance jeudi et vendredi:

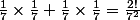
Mais là, l'événement c'est: les deux personnes ont des dates de naissance différentes.

anniv de A différent de anniv de B

anniv de B différent de anniv de A

A né jeudi et B né vendredi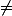

B né jeudi et A né vendredi

Donc pas d'ordre pour notre exercice.

par **nox** » 11 Sep 2006, 09:01

salut

je pense que ce lien peut aider :
http://fr.wikipedia.org/wiki/Paradoxe_des_anniversaires

par **Flodelarab** » 11 Sep 2006, 10:32

nox a écrit:salut

je pense que ce lien peut aider :
http://fr.wikipedia.org/wiki/Paradoxe_des_anniversaires

très joli lien!

Mais ce qu'il n'explique pas, c'est le pkoi de l'arrangement!
Ils introduisent un ordre par faute de raisonnement. Mais cette faute arrange tout le monde. Donc personne dit rien.

Mais je rappelle quand meme que la seule différence entre la combinaison et l'arrangement, c l'ordre! Et pour moi, pas d'ordre donc combinaison.

Je peux très bien faire rentrer m personnes dans une salle simultanément (avec une grosse porte), leur faire tirer une boule dans un saladier (gros egalement) de 365 boules sans avoir noté l'identité de personne ... Je n'aurais donc aucune idée de l'ordre....

A 2 personnes c marrant; Mais la ou ça devient burlesque, c que pour 3 personnes g une probabilité de + de 80% d'avoir le meme anniv. N'importe koi!

OU EST L'ORDRE ? (et la discipline ?)

par **nox** » 11 Sep 2006, 10:48

Flodelarab a écrit:OU EST L'ORDRE ? (et la discipline ?)

:ptdr:

ba j'avoue que j'ai pas cherché aussi loin...ca me parait logique :
méthode BancH

problème à l'envers -> ca me parait bien

probabilité que k personnes aient leurs annivs un jour différent :
la premiere a 365 choix, la 2eme 364, la troisieme 363 etc...jusqu'à 365-k+1 et toujours sur 365 possible.

Donc 365*364*363*.....*(365-k+1)/365^k c'est à dire 365!/(365-k)!*1/365^k

nan ?

par **Flodelarab** » 11 Sep 2006, 10:59

nox a écrit::ptdr:

ba j'avoue que j'ai pas cherché aussi loin...ca me parait logique :
méthode BancH problème à l'envers -> ca me parait bien

probabilité que k personnes aient leurs annivs un jour différent :
la premiere a 365 choix, la 2eme 364, la troisieme 363 etc...jusqu'à 365-k+1 et toujours sur 365 possible.

Donc 365*364*363*.....*(365-k+1)/365^k c'est à dire 365!/(365-k)!*1/365^k

nan ?

Voila pkoi je parle de faute de raisonnement.
Le fait de faire tirer les personnes les une après les autre introduit un ordre dans le calcul a ton insu.

Mais evidemment, ça marche. Donc tout le monde s'en cogne.
Mais ya un pb

par **alben** » 11 Sep 2006, 11:39

Bonjour Flodelarab

L'ordre est dans le 365^m.
Car c'est bien le nombre de possibilités de m anniversaires en tenant compte de l'ordre.
Autrement dit avec 2 personnes, en prenant 365² tu comptes bien A=15 janv et B=25 juin comme différent de A=25juin et B=15janv

par **Flodelarab** » 11 Sep 2006, 12:34

[B]BINGO !!![/B]

Merci beaucoup Alben !

T un chef!

par **BancH** » 11 Sep 2006, 15:04

C'est vrai que c'était dûr à comprendre que l'ordre éait dans le

Tu avais raison de te révolter Flodelarab :++:

Petite probabilité

petite probabilité

Qui est en ligne