Petite pensée sur les intégrales

par **Nightmare** » 21 Déc 2009, 18:22

Salut à tous :happy3:

Je considère f une fonction Riemann-intégrable sur un compact [a,b] et g une fonction dérivable sur [a,b] et à valeur dans ce même segment.

On subdivise le segment

en

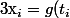L'intégrale de f sur [a,b] est la limite de la somme

(1) avec

pour

bien choisis.

Ceci étant dit, le TAF nous assure qu'il existe

tel que

et en prenant

, la somme (1) tend vers

.

Ceci prouve donc la formule de changement de variable.

Peut-on dans le même genre d'idée montrer la formule d'intégration par partie?

par **Nightmare** » 21 Déc 2009, 18:23

Il y a une petite arnaque dans ma preuve, on a besoin d'une hypothèse supplémentaire sur f pour que la démo soit vraie.

par **Arkhnor** » 21 Déc 2009, 19:06

Salut. :)

Je ne sais pas trop, par contre, avec la même méthode, on peut démontrer le théorème fondamental du calcul, avec pour hypothèses que f' est Riemann-intégrable.

par **Nightmare** » 22 Déc 2009, 14:23

Salut :happy3:

Oui, et monotone comme ici (pour garder la subdivision)

En fait je me demande vraiment si on peut démontrer tous les théorèmes de la théorie de Riemann sans utiliser justement le théorème fondamental mais juste avec la construction de celle-ci.

par **Arkhnor** » 22 Déc 2009, 17:55

Pas besoin de la monotonie.
En fait, la construction de l'intégrale de Riemann(-Stieltjes) comme je la connais se fait avec les sommes inférieures et supérieures de Darboux.
La convergence des sommes de Riemann est vu comme une propriété.(équivalente à la définition)

par **Nightmare** » 22 Déc 2009, 17:59

Arkhnor > Oui, j'ai vu la même construction en sup(c'est d'ailleurs la construction usuelle non?) mais je me rappelle qu'après avoir démontré les propriétés élémentaires (linéarité, etc.) on est passé directement au théorème fondamental liant primitives et intégrales et on a alors démontré les gros théorèmes sur l'intégrale à partir de celui-là et j'ai l'impression qu'on masque un peu le fond de la théorie de Riemann en faisant ça (même si le théorème fondamental est en un sens le coeur de cette dernière).

par **Arkhnor** » 22 Déc 2009, 20:20

Il y a une autre construction, qui consiste à encadrer la fonction par deux fonctions en escalier. (grosso modo)
Ca ressemble aux fonctions réglées, mais c'est bien l'intégrale de Riemann.
Ca permet d'ailleurs de définir l'intégrale de fonctions à valeurs dans un Banach.

Pourquoi supposer f' monotone alors ?

Petite pensée sur les intégrales

Petite pensée sur les intégrales

Qui est en ligne