Petite limite pas gentille

[Epo]

Salut les matheux,

Alors voilà je bloque sur le limite en pi/2 de : ( definit en ]0 - Pi/2[ )



on trouve +inf -inf ; de plus utiliser les DL me semble inapproprié puisque nous somme en pi/2 et avec le taux d'accroissement finit je trouve des choses trop bizarre.

Merci pour le coup de main

( Ps : au passage si quelqu'un à une relation entre le DL à l'ordre 2 en 0 de tan(x+ pi/4 ) ( soit le Dl en pi/4 de tanx non ? ) et le DL à l'ordre 2 de cosx cos²x et cos-²x ca m'enleverai un autre épine du pied )

Merci d'avance !

[Pythales]

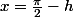
Je pose avec
L'expression devient
Il ne reste plus qu'à mettre en facteur au numérateur, et en facteur au dénominateur ...
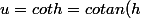Posons pour simplifier Ca donne
avec

[Epo]

Je vais peut être dire une bétise mais... c'est quoi coth ? et je suis totalement perdu :/

on pose x et on devrais avoir tan ( pi/2 - h ) pourquoi ca devient coth ?

et comment passe tu de l'égalité de gauche à celle de droite ?

et pourquoi mettre en facteur alors que c'est des + et - et numérateur et dénominateur ?

[Ericovitchi]

Et au passage :





cot c'est cotangente, = 1/tan

[arnaud32]

[Epo]

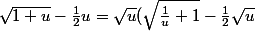ALors je suis d'accord mais avec les limite on se retrouve avec +inf ( 1 -inf ) non ?



Pour coth c'est une notion que je n'ai pas encore vu donc je pense que je ne peut pas l'utiliser dans mon exo :/

[arnaud32]

oui et
+1-inf= -inf
et
(+inf)*(-inf)= -inf
non?

[Epo]

oui et
+1-inf= -inf
et
(+inf)*(-inf)= -inf
non?

Ha bha oui ^^' c'est pas l'addition Merci beaucoup pour cette limite

Maintenant il me reste cette relation entre DL0 tan(x + Pi/4 ) et DLpi/4 cosx cos²x et cos-² :/

[Ericovitchi]

je te les ai tous donné dans mon précédent post

[arnaud32]

tu peux partir de si tu ne veux pas des belles formules qui t'ont ete donnees precedement.

[Epo]

->certes mais une est en pi/4 et les 3 autre en 0, de plus ou est la relation entre tan et les autre ?
->tan²x ce n'est pas tan nop ?

[Ericovitchi]

non je t'ai donné celui de tan (x+pi/4) au voisinage de 0, c'est ce que tu avais demandé.

Sinon je n'ai pas bien compris ce que tu cherchais au juste avec ces DL donc je ne peux pas te répondre. Tu cherches des relations entre ces DL ?

(et sinon 1+tan²x = 1/cos²x et comme je t'ai donné celui de 1/cos²x, tu as celui de tan² x)