Petite intégrale trigonometrique!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 08:50
bonjour!
voilà l'intégrale que j'étudie, j'ai fais un changement de variable
x=
j'obtiens comme intégrale
peut etre ce n'était pas le bon changement de variable!
Je pense pas que c'est juste et si par hasard c'est bon ce que j'ai fais, je vois pas ce que je peux faire maintenant!
merci d'avance
-
mathelot
par mathelot » 24 Aoû 2009, 09:02
bonjour,
poser
-
sasie
- Membre Naturel
- Messages: 21
- Enregistré le: 16 Aoû 2009, 12:47
-
par sasie » 24 Aoû 2009, 09:33
mathelot a écrit:bonjour,
poser
bonjour, pourquoi tu le sais ca ?
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 09:35
merci,
j'ai calculé et je trouve
je ne suis pas sûre que cela soit juste en plus la fonction n'est pas pair ni impaire ..
-
mathelot
par mathelot » 24 Aoû 2009, 09:55
ditans a écrit:
bah non.
en fait, poser
est mieux.
içi et
=sin(\frac{\pi}{4})=\frac{1}{ \sqrt{2}})
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 10:58
merci,
mais ensuite j'obtiens cos ( t -
)
est ce que je developpe à l'aide de cos (a -b) ?
car j'obtiens encore quelque chose de bizarre si je fais ca en haut et en bas!
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 24 Aoû 2009, 11:12
ditans a écrit:merci,
mais ensuite j'obtiens cos ( t -
)
est ce que je developpe à l'aide de cos (a -b) ?
car j'obtiens encore quelque chose de bizarre si je fais ca en haut et en bas!
C'est-à-dire?
-
mathelot
par mathelot » 24 Aoû 2009, 11:22
avec tes notations:
ditans a écrit:voilà l'intégrale que j'étudie, je fais un changement de variable
t=
il n'y a absolument aucun problème théorique. :hum:
l'ancienne variable se nomme
.
la nouvelle variable se nomme
Il s'agit d'une vulgaire translation.
on calcule l'ancienne variable x en fonction de la nouvelle variable t. :hum:
On utilise les identités trigonométriques pour développer les calculs :hum:
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 11:41
}{sin(t-\frac{\pi}{4}) + cos(t-\frac{\pi}{4}) dt)
ensuite je développe
 = sin t cos {\frac{\pi}{4}} - sin {\frac{\pi}{4}} cos t)
de même pour cos
sachant que
je peux donc factoriser par
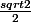
}{\frac{sqrt{2}}{2}(sin t - cos t + cos t - sin t ) dt)
=S
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 24 Aoû 2009, 11:47
Il y a un problème dans le développement de
)
: on a
 = \frac{\sqrt 2}2\(\cos x +\sin x\))
(comme tu l'as écrit on aurait une division par
).
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 12:03
girdav a écrit:Il y a un problème dans le développement de
)
: on a
 = \frac{\sqrt 2}2\(\cos x +\sin x\))
(comme tu l'as écrit on aurait une division par
).
}{\frac{sqrt{2}}{2}(sin t - cos t )+ {\frac{sqrt{2}}{2}}{(cos t - sin t ) dt)
ca vient au même non ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
par girdav » 24 Aoû 2009, 12:08
ditans a écrit:}{\frac{sqrt{2}}{2}(\sin t - \cos t )+ {\frac{\sqrt{2}}{2}}{(\cos t + \sin t ) dt)
ca vient au même non ?
Il y a donc un plus, ce qui permet des simplifications.
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 12:34
girdav a écrit:Il y a donc un plus, ce qui permet des simplifications.
aah oui autant pour moi !! merci!
j'obtiens
}{{sqrt{2}} sin t }dt)
=S
-
mathelot
par mathelot » 24 Aoû 2009, 12:42
ditans a écrit:aah oui autant pour moi !! merci!
j'obtiens
=S
bon, ce n'est pas mal. j'espère que tu as vérifié les calculs.
on divise chaque terme de la somme par sint
on factorise les constantes devant l'intégrale.
le deuxième terme est de la forme
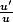
on pouvait poser aussi
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 13:18
[quote="mathelot"]bon, ce n'est pas mal. j'espère que tu as vérifié les calculs.
on divise chaque terme de la somme par sint
on factorise les constantes devant l'intégrale.
le deuxième terme est de la forme
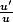
QUOTE]
merci donc en divisant chaque terme de la somme par sin t
ayant pas le droit d'enlever le 1 ou le mettre devant l'intégrale ... je ne sais ps quoi faire
merci beaucoup en tout cas!!!
-
mathelot
par mathelot » 24 Aoû 2009, 13:22
parfait.
l'intégrale d'une différence est la différence des intégrales.
on dit que l'intégrale est une "forme linéaire"on primitive la fonction constante 1
on primitive aussi la fraction
dee la forme
-
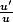
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 13:29
ah oui, je cherchais trop compliqué, tandis que c'est letape la plus facile!!!
merci beaucoup, esperons que j'arriverai à le faire toute seule en DS ^^
-
grikor
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Mai 2009, 16:39
-
par grikor » 24 Aoû 2009, 13:30
bonjour,
poser tg(x/2)=t, sinx=2t/(1+t²);cosx=...
-
ditans
- Membre Relatif
- Messages: 107
- Enregistré le: 15 Aoû 2009, 17:27
-
par ditans » 24 Aoû 2009, 13:51
bonjour
encore une question, voici presque la même intégral
j'ai fai un changement de variable x= t-
, le même que celui auparavant, et je trouve exactement la même solution. Est ce que c'est normal ?
mercii!!!
-
mathelot
par mathelot » 24 Aoû 2009, 14:02
ditans a écrit:bonjour
encore une question, voici presque la même intégral
j'ai fai un changement de variable x= t-
, le même que celui auparavant, et je trouve exactement la même solution. Est ce que c'est normal ?
mercii!!!
la somme des deux intégrales vaut la primitive de 1 :we:
par linéarité, comme on dit.
soit
ps: connais tu une primitive de
}{sin(t)})
?
elle s'écrit agréablement avec un log et une valeur absolue.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
