Petit théorème de Fermat [licence]

[mathelot]

Bjr tous,

Le petit théorème de Fermat indique:

si p est un entier naturel premier et a un entier naturel non multiple de p,



On raffine ce théorème par celui plus fort du à Euler:

si a et p sont des entiers naturels quelconques,
si gcd(a,p)=1



Ma question est la suivante:
l'entier a peut il être d'ordre strictement inférieur à ?

merçi pour le contre-exemple.

[yos]

l'entier a peut il être d'ordre strictement inférieur à ?

Déjà si a=1...
Sinon dans Z/7Z, l'élément 2 est d'ordre 3.

[ThSQ]

l'entier a peut il être d'ordre strictement inférieur à

Absolument : http://en.wikipedia.org/wiki/Carmichael_function

[mathelot]

euh,

il faut que je regarde des exemples à la calculatrice. En attendant:

1) l'ordre (multiplicatif) d'un inversible de
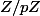
(p quelconque) dépend de .
l'ordre d'un élément inversible particulier pourrait être strictement inférieur à ?

En effet, dans la définition de intervient le quantificateur

2) il me semble avoir lu qu'il y a toujours un générateur du groupe des inversibles de ?

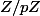
merçi d'avance.

[mathelot]

up....................12 heures plus tard

[abcd22]

Bonsoir,
est le PPCM des ordres des éléments de (Z/pZ)^*, le PPCM de deux nombres n'est pas forcémemt égal à l'un de ces nombres.
Si p est premier, (Z/pZ)^* est un groupe cyclique, autrement dit (Z/pZ)^* est isomorphe à Z/(p-1)Z (cas particulier d'un théorème qui dit : « si K est un corps, tout sous-groupe fini de K^* est cyclique », mais il y a peut-être d'autres démonstrations), mais il n'est pas évident d'en trouver un générateur.