Bonjour,
Le dessin est faux.
Les deux cercles sont tangents en G et les points G,A,I sont nécéssairement alignés, si A et I sont les centres des cercles. :hum:
Dans un premier temps, on choisit un vecteur normé sur la demi-droite
)
que l'on complète pour obtenir un repère orthonormé direct
.)
On pose

rint
Dans ce repère, les coordonnées d'un point M sont notées
.)
B a pour coordonnées polaires:
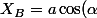)
)
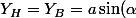)
+r)
On exprime la tangence des deux cercles par:
i) G est aligné avec les centres A et I.
ii)
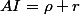
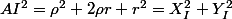
) - a^2 \sin^2(\alpha) \right)}^{\frac{1}{2}})
Par linéarité, sur la droite (AI) passant par l'origine A du repère , G a pour coordonnées:
 = \left( \frac{\rho}{\rho+r} X_{I},\frac{\rho}{\rho+r} Y_{I} \right))
Soit
)
le repère habituel. Un point M a pour coordonnées
)
dans ce repère.
Le changement de base est:
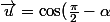 \vec{i}+\sin(\frac{\pi}{2} - \alpha ) \vec{j})
ie,
 \vec{i}+\cos(\alpha ) \vec{j})
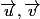
étant orthonormé direct:
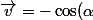 \vec{i}+\sin(\alpha ) \vec{j})
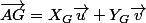
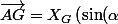 \vec{i}+\cos(\alpha ) \vec{j} \right) +Y_{G} \left( - \cos(\alpha ) \vec{i}+\sin (\alpha ) \vec{j} \right))
Les coordonnées de G dansle repère
)
sont :
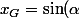 X_{G} - \cos(\alpha) Y_{G})
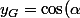 X_{G} + \sin(\alpha) Y_{G})
Cordialement,

