Petit problème complexes trigo

[Abilys38]

Bonjour à tous,
On me demande de résoudre l’équation suivante : √3cos x – sinx = √2
Dans la correction, il est expliqué au départ que :
√3cos x – sinx = 2cos (- π/ 6) + 2 sin (- π/ 6)sin x
Quelqu’un peut il m’expliquer comment en arriver là ?

Merci beaucoup !!

[Sake]

Bonsoir,

sqrt(3) = 2*cos(pi/6) = ???

Même manipulation non triviale pour 1.

[anthony_unac]

Bonjour,

N'hésitez pas à redessiner votre cercle trigonométrique avec les valeurs les plus connues.
Ici en l'occurence, on joue au chat et à la souris avec les angles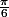 et

PS : Il faut être deux moitiés pour ne former qu'un

[Abilys38]

Bonjour,

Je viens de voir que j'ai fais une petite erreur . Cependant votre proposition est la bonne.
Donc on a √3cos x – sinx = 2cos (- π/ 6)cosx + 2 sin (- π/ 6)sin x = √2

Cependant, à ce moment là, la correction passe directement à:
<=> cos(- π/ 6 + x) = √2/ 2

Je comprend qu'ils aient divisé par deux, et que cos a cos b = cos (a+b), mais je ne comprend pas pourquoi le sin disparait.

Par ailleurs, Anthony, j'ai du mal à jouer au chat et à la souris puisque je n'ai pas parfaitement compris comment ça marche. Je sors à peine des cours de terminal et commence les cours de prépa

Merci pour votre aide

[Pseuda]

Bonjour,

Revois ta formule de cos (a+b) = cos a cos b - sin a sin b.

[Abilys38]

Oui je venais de trouver !! merci !

[Abilys38]

Par contre, aprés plusieurs vérifications.

Je trouve comme résultat π/12 et -5π/12
Le corrigé donne π/12 et 7π/12, or, le deuxième résultat me donne (- racine 2).

C'est bien une erreur de la correction?

[anthony_unac]

Effectivement on aboutirait à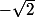
Tes résultats sont corrects
Ne serait ce pas dans la correction ?

[Abilys38]

Non, ils donnent bien " 7π/12 + 2kπ"

[anthony_unac]

Eh bien ils se sont plantés !
La réponse exacte est

[Abilys38]

Mais c'est contradictoire avec mes résultats, non?

[anthony_unac]

Pas du tout, il suffit de prendre et on retrouve ton résultat

[Abilys38]

Ok je pensais que k appartenait à N+

Merci bien

Ceci dit, je serais content de connaître quelques astuces pour mieux maitriser le cercle trigo. J'ai toujours du mal à me repérer.

[anthony_unac]

En trigo, quand on donne l'ensemble des solutions, on donne bien souvent une solution particulière appartenant à 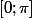ou à laquelle on rajoute 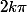ou .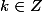
Pour bien se repérer en trigo, il faut dessiner des centaines de fois le cercle avec les valeurs remarquables ( )jusqu'à le visualiser dans ton esprit sans ne plus avoir besoin de le dessiner.
Ensuite quand tu visualiseras bien ça, tu dois être à l'aise avec les formules mélangeant cosinus, sinus, somme, produit (ok il y en a trop).
Faisons le ménage, à quoi bon par exemple s'encombrer l'esprit en retenant par coeur ou autre formule de ce genre sachant qu'en visualisant notre cercle, on le voit très bien donc on le sait .barre !
Essaye de retenir que l'essentiel, sachant que bien souvent il est possible de retrouver une formule grâce à une autre. Trouves donc TON essentiel, les outils indispensables qu'il te faut avoir dans ta boite à outils pour pouvoir résoudre la grande majorité des problèmes.

[Abilys38]

Ok merci pour ce conseil!

[aymanemaysae]

Bonjour;





avec avec ou avec .

[zygomatique]

salut

Bonjour;





avec avec ou avec .

tout d'abord mettre des équivalences ... (sinon il faut revenir en arrière) ...

ensuite un cos x en trop (deuxième ligne) ...

enfin la fonction cos est paire et k varie dans Z donc

a/ +- k2pi est inutile : + k2pi suffit

b/ les solutions sont x + pi/6 = +- pi/4 + k2pi

Dans la correction, il est expliqué au départ que : √3cos x – sinx = 2cos (- π/ 6) + 2 sin (- π/ 6)sin x

il manque évidemment un cos x ...

[aymanemaysae]

Bonjour;

Merci M.Zygomatique pour la remarque, j'ai rectifié l'erreur .

Merci.

[zygomatique]

tu n'as pas rectifié partout ....

[aymanemaysae]

Bonsoir,

Merci pour votre patience. Je crois que maintenant c'est fait!

Encore une fois Merci.