Petit jeu en proba

[bikuta]

Bonjour à tous !
Je suis actuellement en difficulté face à un problème que mon professeur qualifie de simple... Voici l'énoncé.

Un plateau de jeu est numéroté de 1 à n.
On lance un dé à 6 faces équilibré, et on avance du chiffre affiché sur le dé.
On part de la case 1.
Si on tombe sur une case dont le numéro est un nombre premier on perd, et si on arrive jusqu'à n, ou au-delà on gagne.

Quelles est la probabilité de gagner ?

mes recherches
Je comptais utiliser une matrice notée T de transition utilisée dans les chaînes de Markov. Le coefficient aij de la matrice T k correspond à la probabilité d'arriver à la case j en partant de la case i en k coups.

Mon idée étant de remplir la matrice T
par exemple pour n = 4
T =
[ 0 ,1/6,1/6,4/6]
[ 0 , 0 ,1/6,5/6]
[ 0 , 0 , 0 , 1 ]
[ 0 , 0 , 0 , 0 ]

V=
[1]
[0]
[0]
[1]

puis de prendre un vecteur colonne V dont le coefficient vaut 0 si la ligne correspond à un nombre premier, et 1 sinon.
Pour pouvoir ensuite sommer tous les chemins possibles passant par des nombres non premiers en faisant
probabilité_de_gagner = ( T*V+T²*V+T3*V ) [1,1] (le premier coefficient de cette matrice)
mais je trouve une probabilité supérieure à 1 ...

Une autre idée serait d'utiliser seulement le coefficient t1,n qui correspond à la probabilité d'arriver en n en partant de la case 1. En calculant toutes les puissance de T je pourrai trouver la probabilité d'arriver à n en 1,2,...,k coups ! Le seul problème c'est que je ne fais pas intervenir les nombres premiers dans cette matrice T...

J'espère que vous pourrez m'éclairer !
Merci,
Bikuta

[Ben314]

Salut,
On a déjà discuté d'un problème similaire il y a un certain temps, mais je sais plus où (olympiades ? défi ? autres ?)
Par contre ce dont je me souvient, c'est que quelqu'un avait fini par voir que le plus simple et de loin, c'est de partir de la fin, c'est à dire d'évaluer la proba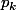 d'arriver à n partant de la case k et évidement, on calcule les pk en partant de la fin.
Tu peut rentrer ça facilement dans un tableur, mais je pense pas que tu puisse trouver une "joulie formule" dépendant de n vu que la répartition des nombres premiers, y'a pas de "joulie formule"...

EDIT : j'ai retrouvé la discution en question (c'était un exo. du concours général 2013 en fait) et c'était nodjim qui avait eu l'idée lumineuse de partir de la fin.

[bikuta]

Merci beaucoup Ben, je vais regarder ça !