UN petit exo sur les endomorphismes

[pouik]

Bonjour,
La reprise est un peu dur avec l'algèbre... :hum: Voilà j'ai quelques difficultés sur l'exercice suivant, donc si vous pouviez m'aider, ce serait formidable. Merci d'avance.

Soit un -espace vectoriel de dimension finie, soit un endomorphisme de . Pour tout entier naturel , on note .
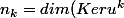1. Montrer que la suite est croissante, et qu'elle est stationnaire à partir du rang , où

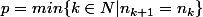
2. Montrer que .

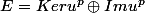
[fahr451]

bonjour

la croissance c 'est facile non ?

[yos]

Bonjour.
L'inclusion est évidente : prends x à gauche et applique lui .

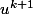
[pouik]

I faut montrer que l'on a :


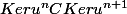
Soit
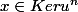
On a donc :

d'où :
or endomorphisme donc est linéaire d'où :

soit

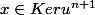
donc

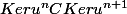
ce qui se traduit au niveau des dimensions par :
,
soit

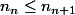
donc est croissante,
non ??

[fahr451]

oui

maintenant montre que la suite ne peut pas être strictement croissante jusqu'au rang n+1 (n = dim E )

[yos]

c'est bon. Elle est stationnaire car majorée donc convergente (et comme c'est une suite d'entiers).

[pouik]

c'est bon. Elle est stationnaire car majorée donc convergente (et comme c'est une suite d'entiers).

désolé mais je ne comprends pas bien pourquoi elle est majorée !!

[SimonB]

T'auras du mal si ton e.v. est de dimension finie à faire grandir des dimensions de noyaux au-delà de la dimension dudit.

[pouik]

Auriez vous une petite idée pour la 2. ?? :zen:

[kazeriahm]

salut

si x est dans l'intersection de Ker u^p et Im u^p,

alors x=u^p(t) (car x est dans Im u^p)

donc u^p(x)=0=u^2p(t)

donc t est dans Ker u^2p =Ker u^2p-1 =...=Ker u^p

donc x=0.

Donc l'intersection = {0}

On conclue par le th du rang

[pouik]

Merci mais je ne comprends pas très bien ce passage :

salut

si x est dans l'intersection de Ker u^p et Im u^p,

alors x=u^p(t) (car x est dans Im u^p)

donc u^p(x)=0=u^2p(t)

donc t est dans Ker u^2p =Ker u^2p-1 =...=Ker u^p

donc x=0.

Donc l'intersection = {0}

On conclue par le th du rang

[kazeriahm]

on sait qu'à partir du rang p, la suite (n_k) est stationnaire.

C'est à dire, pour tout k>=p, n_k=n_p.

En particulier, pour k=2p, on a n_2p=n_p.

Or comme ker u^p C ker u^2p donc keru^p = ker u^2p

?!