Petit exo d'algèbre linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 01 Déc 2007, 18:55
par pouik » 01 Déc 2007, 18:55
Bonsoir,
On note

l'ensemble des suites réelles
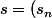_{n \in N})
vérifiant
 \in (R_+^*)^2, \forall n \in N, |s_n| \le M K^n)
1. Montrer que

a une structure de

-espace vectoriel.
2. On considère la loi
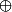
sur
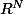
définie par
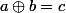
tel que, pour tout

entier naturel,
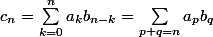
a. Montrer que

est stable pour la loi
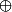
.
b. Déterminer un élément neutre pour la loi
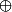
sur

, on le notera

.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 01 Déc 2007, 19:01
par pouik » 01 Déc 2007, 19:01
Donc pour la 1. je propose :
- la suite nulle appartient à

donc

est non vide.
-
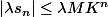
donc en particulier il existe
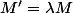
tel que l'on ait :
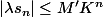
- enfin on a :
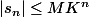
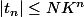
d'où, par somme :
 K^n)
d'où, par l'inégalité triangulaire :
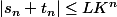
avec
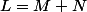
d'où la structure de R-ev. est ce correct ? :we:
-
klevia
- Membre Relatif
- Messages: 318
- Enregistré le: 04 Oct 2007, 20:00
-
 par klevia » 01 Déc 2007, 19:15
par klevia » 01 Déc 2007, 19:15
bonsoir,
Il me semble que M et K dependent de (s) donc pour la stabilité par +, il faut prendre K et K' et prendre le Sup (K,K')
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 01 Déc 2007, 19:27
par aviateurpilot » 01 Déc 2007, 19:27
pour
1) c'est ce que je ferai a ta place.
2)a. supposons que
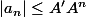
et
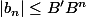
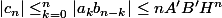
ou
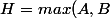,H'=A'B')
donc
^n) b.
b.si

est l'elt neutre alors
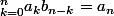
on prend donc
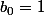
et
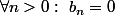
et ona a bien
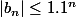
donc
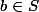
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 01 Déc 2007, 20:06
par pouik » 01 Déc 2007, 20:06
Merci, mais je ne comprends pas :
^n)
Et puis-je me permettre de vous soliciter pour deux petites questions encore. Votre aide m'est très précieuse... j'ai bien compris grace à vous. Merci d'avance.
1. Soit
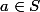
tel que
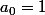
. Montrer qu'il existe une unique suite
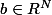
telle que
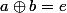
.
2. Soient
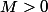
et
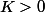
tels que
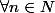
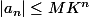
. Montrer que
^n K^n)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 02 Déc 2007, 10:54
par pouik » 02 Déc 2007, 10:54
Bonjour,
Pourriez vous m'aider à resoudre ces dexu questions car je ne vois vraiemnt as comment je dois procéder !! Merci d'avance.
:zen:
pouik a écrit:1. Soit
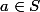
tel que
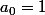
. Montrer qu'il existe une unique suite
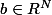
telle que
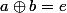
.
2. Soient
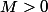
et
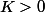
tels que
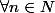
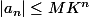
. Montrer que
^n K^n)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 02 Déc 2007, 12:23
par aviateurpilot » 02 Déc 2007, 12:23
pouik a écrit:Merci, mais je ne comprends pas :
^n)
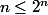
donc
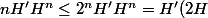^n)
pour les question 1.2.
1.
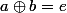
supposons que
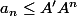
et
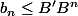
pour
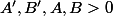
et on prend
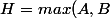)
on a donc
\le A'+B')
donc
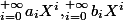
exists
on considere alors les deux application
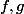
de classe

sur
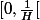
tel que
=\bigsum_{i=0}^{+\infty}a_iX^i,g(x)\bigsum_{i=0}^{+\infty}b_iX^i)
g(x)=\(\bigsum_{i=0}^{+\infty}a_iX^i\)\( \bigsum_{i=0}^{+\infty}b_iX^i\)\\=\bigsum_{i=0}^{+ \infty}\(\bigsum_{p+q=i}a_pb_q\)X^i\\=\(\bigsum_{i=0}^{+\infty}e_iX^i\)\\=1)
on a donc
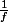
developpable en serie entier et
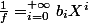
(j'ai pas bien lu mon cours des serie entiers, mais si le developpelement en serie entiers d'une fonction de classe

unique on aura l'unicité des
)
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités