Un petit exercice que je ne comprends pas

[Doraki]

Non, un espace vectoriel a une loi de composition interne "+", et une loi de composition externe "."
tu prends un réel ;) et un élément f de R^R, et tu obtiens ;).f, un nouvel élément de R^R

D'ailleurs je ne sais pas pourquoi tu tiens à prendre X = R. X ça peut être n'importe quel ensemble. Et si tu prends X = n'importe quoi d'autre que R, ça n'a aucun sens de vouloir parler de la loi °

Concrètement, c'est quoi "+" ? dans le cas de X = R, ça veut dire quoi (la fonction x -> 2x+7) "+" (la fonction y -> y²) ?

[capitaine nuggets]

Non, un espace vectoriel a une loi de composition interne "+", et une loi de composition externe "."
tu prends un réel et un élément f de R^R, et tu obtiens .f, un nouvel élément de R^R

D'ailleurs je ne sais pas pourquoi tu tiens à prendre X = R. X ça peut être n'importe quel ensemble. Et si tu prends X = n'importe quoi d'autre que R, ça n'a aucun sens de vouloir parler de la loi °

Concrètement, c'est quoi "+" ? dans le cas de X = R, ça veut dire quoi (la fonction x -> 2x+7) "+" (la fonction y -> y²) ?

Ca signifie

[Doraki]

ok donc ça ça va.

Maintenant tu dois faire quoi pour montrer que R^(X) est un sous espace vectoriel de R^X ?

[capitaine nuggets]

ok donc ça ça va.

Maintenant tu dois faire quoi pour montrer que R^(X) est un sous espace vectoriel de R^X ?

Montrer qu'il est stable par combinaison linéaire.

[alm]

Salut,

Bonjour, j'aimerais faire l'exercice suivant mais je ne le comprends pas :

"Montrer que tout espace vectoriel , toute application "s'étend" de façon unique en une application linéaire de vers ".

Merci d'avance.

Avant de commencer je tiens à dire que arnaud32 avait donné une indication trés utile pour résoudre cette question. C'est la même que je suggère ici mais avec un peu plus de détails
Pour alléger les notations posons .
Pour tout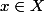 , notons la fonction caractéristique de 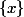, c'est-à-dire que pour tout , on pose .Notons
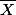Il est aisé de voir que et sont equipotents via l'application: de .
On identifie alors et et on conserve la même notation comme application de
Soit . Alors il existe tel que pour tout et pour tout .
Posons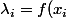 pour tout .
Alors .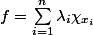
Ceci prouve que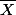 est une famille génératrice de .
Il est facile de prouver que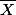 est libre. Aussitôt 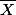est une base de .
C'est ça qui justifie que peut se prolonger de façon unique en une application linéaire de vers .
En effet une application linéaire est complétement déterminée par ses valeurs aux vecteurs d'une base de départ.

Remarque : Il n'est pas necessaire de supposer que est fini.

[capitaine nuggets]

(...) Il est aisé de voir que et sont equipotents via l'application: de .
On identifie alors et et on conserve la même notation comme application de .

Je ne comprends pas ce que signifie le terme "équipotent".
Et je ne comprends pas ton raisonnement, et ce qui t'as permis d'avoir de telles idées.
Pour être plus clair, je ne sais pas de quoi on doit partir, ni de ce qu'on doit obtenir...

[alm]

Salut:
Deux ensembles non vides et sont équipotents s'il existe une bijection .
et sont equipotents car l'application tel qe pour tout est bijective.

[alm]

Salut
Pour la libérté de si sont des éléments deux à deux distincts de et des scalaires tel que alors pour tout on a . Or , puisque pour on sait que , donc les sont tous nuls.

[barbu23]

Je suis un peu perdu là, @Mohammed, tu n'as fait que montrer que admet une base, non ?
D'abord, il faut montrer l'existence de , ensuite montrer qu'il est unique, ensuite, montrer que la restriction de à est , non ? Il faut passer par toutes ces étapes, non ?

[alm]

Salut

Je suis un peu perdu là, @Mohammed, tu n'as fait que montrer que admet une base, non ?
D'abord, il faut montrer l'existence de , ensuite montrer qu'il est unique, ensuite, montrer que la restriction de à est , non ? Il faut passer par toutes ces étapes, non ?

Je n'ai pas à démontrer tout ça car j'ai utilisé un théorème fondamental en algébre linéaire:

Théorème:
Soient et deux espaces vectoriels, une base de et une famille de vecteurs de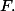
Il existe une et une seule application linéaire de vers tel que:


Je suppose ce théorème connu, sinon voici explicitement la définition de :
Si avec alors

Dans le cas de notre exo avec l'identification de et :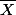
Si un vecteur de s'écrite alors
Pour la restriction à c'est clair : si 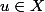alors les coordonnées de sont avec (symbole de Kronnecker)

Mise en garde : les sommes ci-dessus ont un sens car les familles de scalaires utilisées sont toutes à support fini.

[alm]

Pour être plus clair, je ne sais pas de quoi on doit partir, ni de ce qu'on doit obtenir...

Depart ::
Une application

Arrivée :
Une application linéaire tel que :
où

Réponse suggérée:
Pour tout , on identifie et ( est l'application de tel que pour tout on a : si et sinon: identification légitime car et sont équipotent (en bijection))
Si alors s'écrit de façon unique où la famille de scalaires est à support fini (ce qui veut dire : seulement un nombre fini de sont non nuls) On pose :