Un petit exercice que je ne comprends pas

[capitaine nuggets]

Bonjour, j'aimerais faire l'exercice suivant mais je ne le comprends pas :

"Montrer que tout espace vectoriel , toute application "s'étend" de façon unique en une application linéaire de vers ".

Merci d'avance.

[arnaud32]

tu peux peut etre considerer
telle que ou=1 si x=a et 0 sinon

[Doraki]

est-ce que X est fini ?

[capitaine nuggets]

est-ce que X est fini ?

Oui, X est supposé fini.

Par contre, je ne comprends ni la phrase, ni le sens du mot "étendre" ici.
Et donc, ton explication arnaud32
Tu pourrais m'éclairer ?

[Doraki]

Ici on identifie implicitement X à un sous-ensemble de R^X, en identifiant un élément a de X à la fonction fa qui à x associe 1 si x=a et 0 sinon.

Une fois qu'on a ça la question est de savoir si il existe une fonction linéaire ;) de R^X (qui est implicitement un espace vectoriel) dans V, qui étend ;), c'est à dire telle que ;)(fa) = ;)(a) pour tout a de X, et si oui combien il y en a.

[capitaine nuggets]

Ici on identifie implicitement X à un sous-ensemble de R^X, en identifiant un élément a de X à la fonction fa qui à x associe 1 si x=a et 0 sinon.

Une fois qu'on a ça la question est de savoir si il existe une fonction linéaire de R^X (qui est implicitement un espace vectoriel) dans V, qui étend , c'est à dire telle que (fa) = (a) pour tout a de X, et si oui combien il y en a.

Alors là, aucune idée.
Je ne saisis absolument pas ce que tu essaies de me dire :doh:
Peut-être pourrions-nous répondre à cette question en faisant quelques exemple avant pour me permettre de mieux comprendre l'exercice et ainsi avoir des idées, parce que là, c'est le vide total.

[capitaine nuggets]

Ici on identifie implicitement X à un sous-ensemble de R^X, en identifiant un élément a de X à la fonction fa qui à x associe 1 si x=a et 0 sinon.

Une fois qu'on a ça la question est de savoir si il existe une fonction linéaire de R^X (qui est implicitement un espace vectoriel) dans V, qui étend , c'est à dire telle que (fa) = (a) pour tout a de X, et si oui combien il y en a.

Alors là, aucune idée.
Je ne saisis absolument pas ce que tu essaies de me dire :doh:
Peut-être pourrions-nous répondre à cette question en faisant quelques exemple avant pour me permettre de mieux comprendre l'exercice et ainsi avoir des idées, parce que là, c'est le vide total.

Pendant que j'y pense, que signifie ?

[Doraki]

Vérifier qu'on sait de quoi parle l'exercice c'est un truc qu'on fait avant de commencer à réfléchir.

R^X est l'ensemble fonctions de X dans R.

[capitaine nuggets]

Vérifier qu'on sait de quoi parle l'exercice c'est un truc qu'on fait avant de commencer à réfléchir.

R^X est l'ensemble fonctions de X dans R.

oui, ça je le savais, mais ce que je ne savais pas, c'est que .

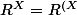Qu'entends-t-on par "étendre" ?

[barbu23]

Je pense qu'il y'a une différence entre et
est l'ensemble des fonctions .
est l'ensemble des familles presque nulles tel que :
Donc, il y'a une différence, non ?

[Doraki]

ben moi j'ai jamais vu cette notation "R^(X)".
si A,B,C sont trois ensembles et A est inclus dans B, une fonction f : A -> C étend une fonction g : B -> C, ça veut dire que g est la restriction de f à B (pour tout x de B, f(x)=g(x))

Je pense qu'il y'a une différence entre et
est l'ensemble des fonctions .
est l'ensemble des familles presque nulles tel que :
Donc, il y'a une différence, non ?

Ici, il a dit que X était fini donc si c'est ce que tu dis, il n'y a pas de différence.

[capitaine nuggets]

est l'ensemble des familles presque nulles tel que :

Oui, voilà c'est la définition que je cherchais !
Mais je ne la comprends pas bien, tu pourrais le l'expliquer s'il te plait.

[Doraki]

Ca veut dire une fonction a : X -> R, telle que {x:X / a(x) <> 0} est un ensemble fini.
Si on a une famille presque nulle à valeurs dans un espace vectoriel, on peut alors définir sa somme en disant qu'on somme les termes non nuls. comme il y en a qu'un nombre fini, il n'est donc pas question de somme infinie ou de limite.

[capitaine nuggets]

Ca veut dire une fonction a : X -> R, telle que {x:X / a(x) 0} est un ensemble fini.

Désolé, je ne comprends pas tes notations :triste:

[Doraki]

l'ensemble des éléments x de X tels que a(x) est différent de 0 est un ensemble fini.

[capitaine nuggets]

l'ensemble des éléments x de X tels que a(x) est différent de 0 est un ensemble fini.

Comme par exemple :
si et si

[Doraki]

Avec quel X ?

Aussi, c'est pas totalement trivial de vérifier que R^(X) est un sous-espace vectoriel de R^X.
Si tu ne l'as jamais vu il faut que tu te poses la question.

[capitaine nuggets]

Avec quel X ?

Aussi, c'est pas totalement trivial de vérifier que R^(X) est un sous-espace vectoriel de R^X.
Si tu ne l'as jamais vu il faut que tu te poses la question.

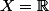
En prenant , ca marche ?

Je l'ai vu en ce début d'année. Mais je ne savais pas que est un sev de .

Mais je pense que ce serait une bonne chose de le montrer.
Toutefois, je ne vois pas comment commencer...

[Doraki]

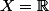
En prenant , ca marche ?

Ben généralement quand on définit une fonction on donne l'ensemble de départ, l'ensemble d'arrivée, puis la relation. Là tout ce que t'as donné c'est une relation vague.
Mais oui, si tu prends une fonction de R dans R, qui à 0 et 1 associe deux réels non nuls, et qui à tous les autres réels associe 0, tu obtiens une fonction "presque-nulle" (ou une famille "presque-nulle" c'est pareil), c'est-à-dire un élément de R^(R).

Mais je pense que ce serait une bonne chose de le montrer.
Toutefois, je ne vois pas comment commencer...

Tu commences par rappeler quelles sont les lois + et . de l'espace vectoriel des fonctions de R dans R, puis tu rappelles la définition d'un sous-espace vectoriel.

[capitaine nuggets]

Ben généralement quand on définit une fonction on donne l'ensemble de départ, l'ensemble d'arrivée, puis la relation. Là tout ce que t'as donné c'est une relation vague.
Mais oui, si tu prends une fonction de R dans R, qui à 0 et 1 associe deux réels non nuls, et qui à tous les autres réels associe 0, tu obtiens une fonction "presque-nulle" (ou une famille "presque-nulle" c'est pareil), c'est-à-dire un élément de R^(R).


Tu commences par rappeler quelles sont les lois + et . de l'espace vectoriel des fonctions de R dans R, puis tu rappelles la définition d'un sous-espace vectoriel.

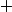
L'ensemble muni des lois de compositions internes et forme un espace vectoriel.

est un sev de ssi
.

Ai-je bon jusque là ?