Petit exercice de géométrie pour se détendre...

[totolito]

(Re)Bonjour

J'espère pouvoir décrire suffisamment le problème pour qu'il soit compréhensible.


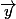
Donc, soit deux repères orthonormés R1 et R2, dont les axes sont colinéaires.
Un plan P est défini dans le repère R1 par un point B et une normale

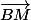
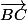
Un vecteur est définit dans le repère R2.
Ce vecteur est dans le plan P.

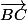
Je cherche à exprimer dans le repère R1.


J'ai essayé de résoudre ce problème en exprimant le plan dans les deux repères à l'aide des équations cartésiennes mais ça n'a mené à rien que je sache exploiter

Encore merci à vous...

[LeJeu]

(Re)Bonjour

J'espère pouvoir décrire suffisamment le problème pour qu'il soit compréhensible.


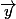
Donc, soit deux repères orthonormés R1 et R2, dont les axes sont colinéaires.
Un plan P est défini dans le repère R1 par un point B et une normale

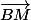
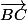
Un vecteur est définit dans le repère R2.
Ce vecteur est dans le plan P.

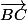
Je cherche à exprimer dans le repère R1.


J'ai essayé de résoudre ce problème en exprimant le plan dans les deux repères à l'aide des équations cartésiennes mais ça n'a mené à rien que je sache exploiter

Encore merci à vous...

Bonjour,

C'est la deuxième version que tu donnes de ton' probleme. Et les contraintes changent beaucoup a chaque fois....
Cette version me semble bizarre

Le problème originel c'est quoi .?

[totolito]

Bonjour,

Je reviens avec la solution!

Donc:

- Exprimer C dans le repère R1 à l'aide de ses coordonnées dans R2 et de l'angle Theta entre R1 et R2.
Il s'agit juste d'une rotation d'un angle Theta autour de l'axe des y:
C[x1;y1;z1] = [-z2.sin(Theta) + x2.cos(Theta); y2; z2.cos(Theta) + x2.sin(Theta)]

- Ensuite, puisque le vecteur BC est dans le plan P, alors il est perpendiculaire à la normal au plan P:
Le produit vectoriel BM.BC est donc égal à 0.
Je développe avec les termes de C exprimé dans R1 et je me retrouve avec une identité trigonométrique du type a.cos(Theta) + b.sin(Theta) = 1
qui me permet de déterminer Theta et donc de caculé le vecteur BC dans R1.

CQFD :langue2: