Un pépin avec les noyaux

[Calvinator2000]

Bonjour, je bloque sur une question qui n'a pourtant pas l'air difficile: Soit E un R-espace vectoriel de dimension n. On a préalablement montré que pour tout endomorphisme f de E, il existe un entier k tel que ( 1<=k<=n et E=Ker(f^k);)Im(f^k) ), f^k désigne la composée k-ième de f. Soit p le plus petit entier k verifiant la relation précédente. On suppose p=n. Montrer que f^n est l'endomorphisme nul. Veuillez m'excuser pour l'aspect condensé de mon post mais je l'ai écrit depuis mon téléphone. Merci d'avance pour vos réponses.

[paquito]

Que signifie f^p?,tel que c'est, c'est entièrement faux! Tu prends l'Id déjà,ou un projecteur:et ça tombe à l'eau; sois un peu plus précis.

[Calvinator2000]

Effectivement, j'ai édité mon premier post.

[Ben314]

Salut,
Par hypothèse, on a mais on n'a pas
Or et et, comme , si une des deux inclusion est une égalité, alors l'autre aussi et cela contredirait l'hypothèse. Donc les deux inclusions sont strictes.
Cela signifie en particulier qu'on peut trouver un tel que .
On montre alors aisément que est libre (en appliquant les différents 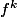à une combinaison linéaire de ces vecteurs) donc c'est une base de E et, comme les images par des vecteurs de cette base sont toutes nulles, ça prouve que (et ça te donne même une base dans laquelle la matrice de est super simple vu qu'elle est entièrement nulle sauf des 1 juste au dessus de la diagonale)

[Calvinator2000]

Merci Ben.