Pavé et lebesgue-négligeabilité

par **legeniedesalpages** » 20 Déc 2007, 23:44

Bonsoir, je ne vois pas comment démarrer pour l'exercice1: :hein:

Définition: Un sous-ensemble

de

est

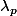
-négligeable quand, pour chaque réel

, il existe une suite

de pavés bornés de

telle que

et

, il existe une famille dénombrable de pavés ouverts bornés de

dont la réunion contient

et dont la somme des

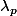
-mesures est strictement inférieure à

.

Merci pour votre aide

par **Lierre Aeripz** » 20 Déc 2007, 23:50

1. Fixe j. Tu sais que tu peux prendre

de mesure arbitrairement proche de la mesure de

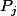
, mais pas égale (pas dur). Prend

, avec

judicieusement choisi.

2. Même idée.

par **legeniedesalpages** » 22 Déc 2007, 20:02

Bonjour Lierre Aeripz,

déjà je bloque pour montrer que pour tout

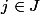
, et pour tout

, il existe un pavé ouvert borné

, tel que

. :hein:

par **legeniedesalpages** » 22 Déc 2007, 20:11

ah si pardon c'est bon :)

par **legeniedesalpages** » 22 Déc 2007, 20:20

ok j'ai compris pour al 1), merci lierre aeripz :)

par **legeniedesalpages** » 23 Déc 2007, 00:43

Un autre exo où je bloque:

Soit un ensemble

qui est

-négligeable. Montrer que, pour

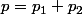
, l'ensemble

est

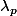
négligeable.

Merci pour vos indications.

par **legeniedesalpages** » 23 Déc 2007, 01:08

en fait c'est bon.

J'ai trouvé en procédant par récurrence sur

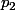
, en utilisant le fait que

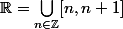
et qu'une réunion dénombrable de négligeables est négligeable.