Passer de coordonnées cartésiennes à polaires

[Sarahm]

Bonjour,
J'ai un exercice qui consiste à trouver la bonne équation d'un cercle (dont on a le graphique) en coordonnées polaires.
La réponse est r=-sin(alpha), ce qui est logique vu qu'en multipliant des deux côtés de l'équation par r, j'obtiens r^2=-rsin(alpha)=-y et je peux donc poser y^2+x^2=-y, et en passant le y de l'autre côtés et avec une complétion du carré, j'arrive à la formule x^2+(y+1/2)^2=1/4, ce qui est bien ce que j'ai sur mon graphique.
Mais j'avais posé avant x^2+(y+1/2)^2=r^2 dans le but de remplacer x par rcos(alpha) et y par rsin(alpha) pour pouvoir trouver une fonction de r en l'isolant. Sauf que quand je fais ça j'obtiens r=1/(4sin(a)), donc pas du tout la réponse que je suis sensée trouver. Je ne comprends pas pourquoi je ne peux pas poser cela comme ça. Merci pour votre aide si vous avez la réponse !!

[GaBuZoMeu]

Bonsoir,

J'ai l'impression que tu te mélanges les pinceaux au sujet de Dans les coordonnées polaires, on a 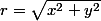, la distance à l'origine.
Quand tu écris , le est le rayon du cercle et n'a rien à voir avec la distance à l'origine du point .

[Sarahm]

Oui c'est ça je me suis méga emmêlé les pinceaux ! Merci beaucoup !! En fait les deux r sont égaux quand le cercle est centré à l'origine n'est-ce pas ?

[GaBuZoMeu]

Certes ...

[Sarahm]

tip top merci !