Parties majorées de Q

[gilles3]

Bonjour,

voilà un théorème très intéressant
Dans Q (rationnels), il existe des parties non vides et majorées qui n'ont pas de borne supérieure.

et voici sa démonstration: hélàs je ne comprends pas toutes les étapes...

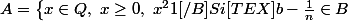
Soit , alors , ce qui équivaut à.

Il suffit donc que , soit.

Avec n dans N vérifiant [1] et [2], on voit que b n'est pas le plus petit élément de B. Je comprends pas du tout le raisonnement

Si vous pouviez m'aider à mieux la comprendre...

Merci beaucoup

[emdro]

Bonjour,

Il s'agit de montrer que B n'a pas de plus petit élément.
Pour cela, on raisonne pas l'absurde en supposant qu'il y en ait un. On l'appelle b. Le raisonnement consiste à chercher un b-1/n (qui est encore rationnel) qui soit toujours dans B, ce qui contredit le fait que b soit le plus petit!

Pour cela on doit à un moment élever b-1/n au carré. Et pour que l'ordre soit conservé, il vaut mieux que b-1/n>0, i.e. bn>1.

OK?

[emdro]

Si , alors , ce qui équivaut à.

A vrai dire, ces étapes (en rouge) du raisonnement sont à revoir, car c'est la réciproque dont on aura besoin: on aura un n suffisamment grand, et il faudra prouver que .

NB Tu avais oublié le carré; je l'ai rétabli.

[wserdx]

Peut-être as-tu besoin de prendre un peu de hauteur par rapport à cette démonstration qui est technique. Il me semble que ce qui est important dans ce théorème, c'est de comprendre la densité de dans .
En particulier, on devine bien que la partie A a bien une borne qui est
mais celle-ci appartient à et pas
L'idée de la démonstration est de montrer qu'on peut trouver des rationnels b
aussi proche de qu'on veut.
Même si b est très près de , (la valeur qui apparait dans la démonstration) peut être très grand, mais on peut trouver plus grand encore.