Partie ouverte

par **barbu23** » 30 Mar 2009, 18:18

Bonjour à toutes et à tous : :happy3:
Soit

muni de la topologie

associée à la metrique usuelle, telle que :

Alors :

:

Je voudrais savoir si :

n'est pas ouvert, et comment peut - t - on le prouver ?
Merci d'avance ! :happy3:

par **Nightmare** » 30 Mar 2009, 19:51

salut :happy3:

Je ne comprends pas le :

par **barbu23** » 30 Mar 2009, 19:56

Salut : :happy3:
Cette ecriture signifie que tout ouvert est reunion quelconque de boule metrique ouvertes !
Cordialement ! :happy3:

par **Nightmare** » 30 Mar 2009, 20:07

D'accord,

et que signifie

?

(Edit : C'est l'indexation qui me chiffonne)

par **barbu23** » 30 Mar 2009, 20:10

Cette écriture signifie : intersection quelconque de complementaires de boules metriques ouvertes de la topologie

. Est ce que c'est un ouvert ? :hein:
Cordialement ! :happy3:

par **Nightmare** » 30 Mar 2009, 20:19

Oui mais je ne comprends pas dans quoi varient x et r !!

Cela veut dire qu'on considère l'intersection des complémentaires de toutes les boules ? Cela m'étonnerait.

par **barbu23** » 30 Mar 2009, 20:29

Non, ça veut dire que , il s'agit d'une intersection quelconque et non au plus denombrable .. celà signifie qu'elle peut être indénombrable, Bref :

et

avec

de cardinal indenombrable ... c'est pas du tout evident ! :hum:
Bref :

est une topologie des boules metriques ouvertes

.. On contruit à partir de cette topologie, une nouvelle topologie

dite topologie des fermés de

formés des parties de

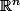
complementaires des boules metriques ouvertes de

.. !
Alors, on essaye de voir ce qui se passe quant on prend une famille quelconque de boules de

et on mets leur intersection ! est ce que l'intersection est un ouvert ? :hein:
Amicalement ! :happy3:
C'est pas évident du tout ! :mur:

par **barbu23** » 30 Mar 2009, 20:45

La question fondamentale surquelle s'appuie tout cet exo est de reussir à prover que les seules parties à la fois ouvertes et fermés de

pour cette topologie donnée sont

et

. :marteau:

par **barbu23** » 30 Mar 2009, 20:56

la reponse est là :
http://forums.futura-sciences.com/mathematiques-superieur/300353-partie-ouverte.html
:lol2:

par **barbu23** » 30 Mar 2009, 21:13

"Nightmare" ! désolé de t'avoir chifonné un peu la tête pour rien ! :hum: j'ai mal exprimé l'idée depuis le départ :
De toute façon :

est connexe, celà veut dire que les seules parties à la fois ouvertes et fermées sont l'ensemble vide et

... et puisque :

est fermé ! pourqu'il soit ouvert il doit être soit egale à

soit à

Amicalement ! :happy2:

par **Nightmare** » 30 Mar 2009, 21:32

Effectivement je n'avais pas compris ton énoncé.

Partie ouverte

Partie ouverte

Qui est en ligne