Partie majorée dans R et Z
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 01 Aoû 2018, 22:46
par mehdi-128 » 01 Aoû 2018, 22:46
Bonsoir,
Soit x un réel quelconque. Soit :

On veut montrer que A est majorée dans
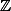
Il est clair que A est majorée dans

par x :

Pour
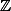
je ne comprends pas ce qui suit :
D'après la propriété d'Archimède il existe un entier plus grand que x donc A est majorée dans 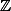
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 01 Aoû 2018, 23:37
par Pseuda » 01 Aoû 2018, 23:37
Bonsoir,
Cela semble pourtant évident. D'après la propriété d'Archimède, il existe n dans Z tel que x<=n. Donc pour tout p dans A, p <=x<=n. Il existe donc n dans Z tel que pour tout p dans A, p<=n. Soit A est majoré dans Z.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 01 Aoû 2018, 23:57
par mehdi-128 » 01 Aoû 2018, 23:57
" D'après la propriété d'Archimède, il existe n dans Z tel que x<=n"Dans mon cours la propriété d'Archimède est :

Et pour x=1 :

Or, le x n'est pas forcément positif, et le n est entier relatif et pas naturel comme dans la propriété.

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 02 Aoû 2018, 00:00
par Pseuda » 02 Aoû 2018, 00:00
Mais pour x<0, le problème est réglé car 0 est dans Z ! Je veux dire par là qu'on n'a pas besoin d'utiliser la propriété d'Archimède dans ce cas.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 02 Aoû 2018, 00:17
par mehdi-128 » 02 Aoû 2018, 00:17
Pourquoi dans le cours c'est
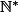
et ici vous utilisez
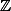
?
Mon livre donne une variante :
Pour les entiers relatifs :

Et pour x=0 ?
Mais je comprends pas comment on l'obtient à partir de l'original....
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 02 Aoû 2018, 08:22
par pascal16 » 02 Aoû 2018, 08:22
pour x=0, n=1 convient
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 02 Aoû 2018, 09:37
par hdci » 02 Aoû 2018, 09:37
Une chose importante sur laquelle vous semblez buter : dans la plupart des cas où on cherche à démontrer "il existe", on parle d'une condition suffisante : inutile de chercher tout ce qui peut marcher, dès qu'on en a trouvé un on peut s'arrêter, c'est suffisant.
Par exemple, est-ce qu'il y a un entier plus grand que -3 ? Oui, par exemple un milliard.
On n'est pas obligé de prendre le "meilleur". J'aurais pu prendre comme entier -2 qui est alors le plus petit entier supérieur strictement à -3, mais un milliard est très bien également, vu que la question est "existe-t-il" et n'est pas "quel est le plus petit entier supérieur".
Revenons à Archimède : comme un entier naturel est un entier relatif, s'il existe un entier naturel plus grand que x, a fortiori il existe un entier relatif plus grand que x : il n'y a qu'à prendre le même.
Se pose ensuite la question des négatifs : et bien par définition même un négatif est majoré par 0 (donc par n'importe quel nombre positif, mais maintenant que j'ai trouvé 0 je n'ai pas besoin d'en chercher d'autres)
Inutile de couper les cheveux en quatre, de se faire des noeuds au cerveau : "existe-t-il", donc "il suffit d'en trouver un" et si on en a déjà trouvé un dans un travail précédent, celui-ci fait bien l'affaire.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 02 Aoû 2018, 09:43
par Pseuda » 02 Aoû 2018, 09:43
pascal16 a écrit:pour x=0, n=1 convient
0 aussi !
si x=<0, A est majoré par 0 qui est dans Z,
si x>0, on utilise la propriété d'Archimède (voir plus haut).
Pas vu le message de @hdci, je laisse.
-
aviateur
 par aviateur » 02 Aoû 2018, 10:17
par aviateur » 02 Aoû 2018, 10:17
Bonjour
Soit x un nombre réel: existe-t-il un nombre entier plus grand que x? Telle est la question.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 02 Aoû 2018, 13:40
par pascal16 » 02 Aoû 2018, 13:40
Si on accepte la notion de "partie entière", il faut 1 ligne
Si on passe par l'écriture décimale (ou tout autre base), c'est fait en une dizaine de lignes.
Si on part du concept de nombre réel comme limite d'une suite de nombre rationnels
-> par division euclidienne, on sait comparer les rationnels aux entiers
-> puis la limite
soit 2 epsilon à ajouter.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 03 Aoû 2018, 01:47
par mehdi-128 » 03 Aoû 2018, 01:47
aviateur a écrit:Bonjour
Soit x un nombre réel: existe-t-il un nombre entier plus grand que x? Telle est la question.
Oui toujours.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 03 Aoû 2018, 01:53
par mehdi-128 » 03 Aoû 2018, 01:53
hdci a écrit:Une chose importante sur laquelle vous semblez buter : dans la plupart des cas où on cherche à démontrer "il existe", on parle d'une condition suffisante : inutile de chercher tout ce qui peut marcher, dès qu'on en a trouvé un on peut s'arrêter, c'est suffisant.
Par exemple, est-ce qu'il y a un entier plus grand que -3 ? Oui, par exemple un milliard.
On n'est pas obligé de prendre le "meilleur". J'aurais pu prendre comme entier -2 qui est alors le plus petit entier supérieur strictement à -3, mais un milliard est très bien également, vu que la question est "existe-t-il" et n'est pas "quel est le plus petit entier supérieur".
Revenons à Archimède : comme un entier naturel est un entier relatif, s'il existe un entier naturel plus grand que x, a fortiori il existe un entier relatif plus grand que x : il n'y a qu'à prendre le même.
Se pose ensuite la question des négatifs : et bien par définition même un négatif est majoré par 0 (donc par n'importe quel nombre positif, mais maintenant que j'ai trouvé 0 je n'ai pas besoin d'en chercher d'autres)
Inutile de couper les cheveux en quatre, de se faire des noeuds au cerveau : "existe-t-il", donc "il suffit d'en trouver un" et si on en a déjà trouvé un dans un travail précédent, celui-ci fait bien l'affaire.
Je vois...
Dans mon cours on donne la propriété d'Archimède pour les réels :

Déjà pourquoi on enlève les réels nuls dans la définition ?
Je comprends pas comment on en déduit les suivantes :
Pour les réels strictement négatifs :

Pour les entiers relatifs :

-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 03 Aoû 2018, 10:02
par pascal16 » 03 Aoû 2018, 10:02
les réels sont non nuls car
x=0 y>0 ne donnerait pas de solution
y=0 : pourrait être intégré
x positif non nul, y quelconque est alors moins restrictif
pour les déductions
la première, c'est la même proposition avec x'=-x et y'=-y
le seconde : avec n dans Z, on s'affranchi du signe
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 03 Aoû 2018, 10:09
par pascal16 » 03 Aoû 2018, 10:09
la seconde serait génréalisable comme ça :

on peut même imposer que |n2-n1|=1
et on retombe sur la notion de "à 2 k pi prés" qui permet de transformer une mesure d' angle en une mesure principale
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 03 Aoû 2018, 12:54
par mehdi-128 » 03 Aoû 2018, 12:54
Ah en fait c'est bon j'ai compris, suffit de prendre -x et -y pour
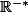
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités