Partie E est Lebesgue-mesurable si et seulement si

[florian1565]

Bonjour,

Je souhaiterai démontrer cette proposition mais je ne vois pas du tout comment procéder :

Une partie E est Lebesgue-mesurable si et seulement si elle s'écrit: E= G \ N avec G un Gδ et N mesurable de mesure nulle, ou de façon équivalente, E = F ∪ N avec F un Fσ et N mesurable de mesure nulle.

Je vous remercie

[Ben314]

Salut,
Tu as quoi comme construction de la mesure de Lebesgue ? (celle avec la notion de "mesure extérieure" ou une autre ?)

[florian1565]

Salut, merci pour ta réponse, celle avec la mesure extérieure

[Ben314]

Dans ce cas là, il me semble que, quasi par définition de la mesure extérieure, pour toute partie E de R^n et tout 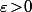, il existe un ouvert U de R^n tel que et .
Ensuite, si tu note U_n un tel ouvert correspondant à puis , alors G est un Gδ contenant E et de même mesure extérieure que E.