Partie entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Aoû 2018, 15:44
par mehdi-128 » 05 Aoû 2018, 15:44
Bonjour,
Soit
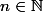
et

la fonction définie de
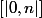
sur

par :
=\binom{n}{k})
J'ai montré que la fonction

est-elle croissante sur
|])
.
Montrer que

est décroissante sur
,n|])
en utilisant la parité des coefficients binomiaux.
J'ai pas compris l'indication.
Merci.
Modifié en dernier par
mehdi-128 le 06 Aoû 2018, 00:01, modifié 1 fois.
-
Viko
- Membre Relatif
- Messages: 209
- Enregistré le: 18 Juin 2017, 23:51
-
 par Viko » 05 Aoû 2018, 15:57
par Viko » 05 Aoû 2018, 15:57
Bonjour,
Cela fait référence à la propriété que je connais personnellement sous le nom de "symétrie des coeffecients binomiaux" et qui dit que
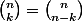
(valable pour tout entier n,k même si k> n ou k < 0)
Qui ne maîtrise pas ses Cassinis, termine à Telecom Nancy
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Aoû 2018, 00:01
par mehdi-128 » 06 Aoû 2018, 00:01
Oui Viko :
=\binom{n}{k}=\binom{n}{n-k})
Mais je vois pas comment l'utiliser ici

-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 06 Aoû 2018, 06:36
par hdci » 06 Aoû 2018, 06:36
Appliquez simplement la définition !
Pour
)
utilisez
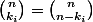
, comparez
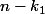
et
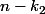
, utilisez la croissance de

pour
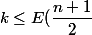
pour obtenir la conclusion
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Aoû 2018, 22:37
par mehdi-128 » 06 Aoû 2018, 22:37
J'ai :
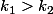
soit :
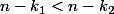
Je prends :
 \leq k_1 \leq n)
et
 \leq k_2 \leq n)
Donc
)
Donc :
)
Je retombe pas sur l'intervalle que je voudrais :
|])
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Aoû 2018, 00:58
par mehdi-128 » 07 Aoû 2018, 00:58
J'ai trouvé la solution :
Si n est pair :
}{2}) = E(\dfrac{(n+1)}{2}) = \dfrac{n}{2})
Si n impair :
}{2}) = \dfrac{(n+1)}{2} > n-E( \dfrac{(n+1)}{2}) = \dfrac{(n-1)}{2})
Donc :
}{2}) \leq E(\dfrac{(n+1)}{2}))
Finalement :
}{2})|] \subset [|0,E(\dfrac{(n+1)}{2})|])
Donc :
 < f(n-k_2))
car f est croissante sur
}{2})|])
Soit :
 < f(k_2))
avec
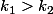

est donc décroissante sur
}{2}),n|])
-
aviateur
 par aviateur » 07 Aoû 2018, 01:14
par aviateur » 07 Aoû 2018, 01:14
Bonjour
Je vais tout de même pas relire tout et puis l'aide que l'on t'a apporté sur le forum
https://forums.futura-sciences.com/mathematiques-superieur/826890-partie-entiere.htmlAvant tout et je te l'ai déjà dit, poses une question par forum mais pas la même question sur des forums différents. Sinon cela devient une vraie salade (surtout dans ta tête) et pardon pour les doublons!
Je ne comprends pas tu calcules le rapport (c'est fait sur l'autre forum) ou la différence de 2 termes consécutifs, comme ci-dessous:
pour
!(n-k-1)!}-\dfrac{n!}{k!(n-k)!})
Et en réduisant au même dénominateur, tu obtiens
!(n-k)!}\times (n-2k))
et cela a le signe de n-2k.
Ce n'est pas la mer à boire de deviner le signe de
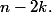
Modifié en dernier par aviateur le 07 Aoû 2018, 01:17, modifié 1 fois.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 07 Aoû 2018, 01:17
par mehdi-128 » 07 Aoû 2018, 01:17
Ok merci finalement j'ai réussi à résoudre l'exercice.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités