A partir de là, ton problème est trivial.
Partie entière
26 messages
- Page 2 sur 2 - 1, 2
Re: Partie entière
Si tu veux pas te prendre la tête (et être efficace dans pas mal de cas), tu as juste à écrire que, de manière générale : 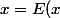 + e) avec
avec 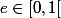 .
.
A partir de là, ton problème est trivial.
A partir de là, ton problème est trivial.
Re: Partie entière
Bonjour;
J'aimerais savoir pourquoi la solution donnée par M.Flemme a été négligée malgré qu'elle a été éditée par celui-ci après la solution qui contenait:
Simple curiosité.
Flemme a écrit:
Et
Donc:
Et puisque :
C'est faux?
J'aimerais savoir pourquoi la solution donnée par M.Flemme a été négligée malgré qu'elle a été éditée par celui-ci après la solution qui contenait:
Flemme a écrit:
Simple curiosité.
Re: Partie entière
1/ si n est entier alors E(n) = n donc on en déduit que E(E(x)) = E(x) (la fonction partie entière est idempotente)
2) la fonction partie entière est croissante
 \le x < E(x) + 1 \\E(y) \le y< E(y) + 1)
on ajoute membre à membre : + E(y) \le x +y < E(x) + E(y) + 2) (*)
(*)
on prend la partie entière + E(y)] \le E(x + y) < E[E(x) + E(y) + 2]) (d'après 2/)
(d'après 2/)
or les extrêmes de (*) sont des entiers donc d'après 1/ : + E(y) \le E(x + y) < E(x) + E(y) + 2)
...
2) la fonction partie entière est croissante
on ajoute membre à membre :
on prend la partie entière
or les extrêmes de (*) sont des entiers donc d'après 1/ :
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Partie entière
Bonjour;
La démonstration de M.Zygomatique m'a émerveillée , mais je me demande encore si la démonstration de M.Flemme est exempte d'erreurs, et si c'est le cas, donc elle a été négligée à tort :
\leq x)
Et
\leq y)
Donc:
+E(y)\leq x+y)
Et puisque :

+E(y)\leq x+y+\varepsilon)
+E(y)-\varepsilon \leq x+y)
+E(y)-\varepsilon \leq E(x+y))
+E(y)\leq E(x+y)+\varepsilon)
La démonstration de M.Zygomatique m'a émerveillée , mais je me demande encore si la démonstration de M.Flemme est exempte d'erreurs, et si c'est le cas, donc elle a été négligée à tort :
Et
Donc:
Et puisque :
Re: Partie entière
Elle a été négligée à raison, car elle ne montre rien de plus que +E(y)\leq E(x+y)) , et ce fait se montre beaucoup plus directement.
, et ce fait se montre beaucoup plus directement.
Re: Partie entière
Bonsoir,
En fait de négligence, c'est plutôt cette 2ème question qui l'a été :
Cette relation est fausse de toute évidence. A revoir donc.
En fait de négligence, c'est plutôt cette 2ème question qui l'a été :
Flemme a écrit:
Et il y a aussi une autre question :
Démontrer que :: xn < E(xn) < xn+1
Mais je croyais que :non ?
Cette relation est fausse de toute évidence. A revoir donc.
26 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
