Bonsoir a tous
s'il vous plait j'aimerais que vous me clarifier une demonstration qu'on a fait en classe .
il s'agit de la demonstration qui dit que card(P(E))=2^n.
en fait le prof l'(a demontrée par réccurrence:
mais je n'ai pas compris son passage au rang n+1.
au départ,on un enemble E à n element.
si n=1 la relation est verifieé
on l'a suppose vérifiée pour un rang n et on démontre qu'elle verifié pour le rang n+1.
donc le prof a considéré un ensemble F et un element a.
il a posé E=FU{a} avec a n'appartenant pas à F.
donc cardE=n+1
il a dit que si G est une partie de F: soit elle est une partie de F :il ya en 2^n possibilité
ou bien elle est partie de FU{a} il y en a egalement 2^n possiblité.
donc le nombre de G est 2^n+2^n=2^(n+1)
mais ce que je n'ai pas compris c'est pourquoi si G est une partie de FU{a} ona 2^n possibilité??? moi je crois plutot que c'est 2^(n+1) possibilite car
Card(FU{a})=n+1.
AIDEZ MOI S'il vous plait
MERCI
Partie du cours ambigue
7 messages
- Page 1 sur 1
Bonsoir,
es-tu familier (/familière) avec la fonction caractéristique?
Je te rappelles quand même ce que c'est:
Soit A une partie de E, on appelle fonction caratéristique de A, notée , la fonction définie sur E, à valeurs dans {0,1}, par:
, la fonction définie sur E, à valeurs dans {0,1}, par:
=\left\{1\mbox{ si }x\in{A} \\ 0\mbox{ si }x\not\in{A}\right) .
.
Si oui, je peux te proposer une démonstration plus simple (selon moi...).
Zeb.
es-tu familier (/familière) avec la fonction caractéristique?
Je te rappelles quand même ce que c'est:
Soit A une partie de E, on appelle fonction caratéristique de A, notée
Si oui, je peux te proposer une démonstration plus simple (selon moi...).
Zeb.
Youpi, amusons-nous!
On va montrer que) , l'ensemble des parties de E, est en bijection avec
, l'ensemble des parties de E, est en bijection avec  , l'ensemble des applications de E dans
, l'ensemble des applications de E dans 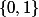 .
.
1- Définition de la bijection
Soit \longrightarrow \{0,1\}^E) ,
,
[INDENT] [/INDENT]
[/INDENT]
On est bien d'accord que ,
,
et que est bien définie (à une partie A de E,
est bien définie (à une partie A de E,  associe une seule application
associe une seule application  ).
).
2- Preuve que est une bijection
est une bijection
a). Montrons que \Phi est surjective
Soit , alors f est une application de E dans
, alors f est une application de E dans 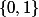 .Posons
.Posons ) . Pour montrer la surjectivité de
. Pour montrer la surjectivité de  , on veut montrer que
, on veut montrer que  , ie
, ie =f(x)) .
.
Soit , si
, si 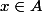 alors, par définition de
alors, par définition de  ,
, =1) . Par ailleurs,
. Par ailleurs, ) donc si
donc si 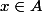 ,
, =1) donc si
donc si 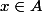 alors
alors =1=f(x)) .
.
Si , alors
, alors =0) par définition de
par définition de  et d'autre part f(x) est différent de 1 par définition de A. Comme f est à valeurs dans
et d'autre part f(x) est différent de 1 par définition de A. Comme f est à valeurs dans 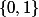 ,
, =0) donc
donc =0=f(x)) .
.
Donc=f(x)) ,
,
donc
et donc est surjective.
est surjective.
b). Montrons que est injective
est injective
Soient ,
,
si=\Phi(B)) , alors
, alors  ,
,
donc quel que soit ,
,  si et seulement si
si et seulement si =1) , si et seulement si
, si et seulement si =1) si et seulement si
si et seulement si  .
.
Donc si=\Phi(B)) , alors A=B
, alors A=B
donc est injective.
est injective.
Et donc est une bijection! Ouf! Beaucoup de lignes pour quelque chose d'évident et même que tu savais peut-être déjà!
est une bijection! Ouf! Beaucoup de lignes pour quelque chose d'évident et même que tu savais peut-être déjà!
3- Calcul du cardinal de)
Le cardinal de est
est  (tu dois le savoir) et on a montré que
(tu dois le savoir) et on a montré que ) est en bijection avec
est en bijection avec  donc...
donc...
le cardinal de) est
est  . :we:
. :we:
On y est arrivé! La démonstration que est bijective est un peu pénible, mais une fois qu'on a vu ça, ça va tout seul!
est bijective est un peu pénible, mais une fois qu'on a vu ça, ça va tout seul!
A bientôt, :++:
Zeb.
On va montrer que
1- Définition de la bijection
Soit
[INDENT]
On est bien d'accord que
et que
2- Preuve que
a). Montrons que \Phi est surjective
Soit
Soit
Si
Donc
donc
et donc
b). Montrons que
Soient
si
donc quel que soit
Donc si
donc
Et donc
3- Calcul du cardinal de
Le cardinal de
le cardinal de
On y est arrivé! La démonstration que
A bientôt, :++:
Zeb.
ferrea a écrit:Bonsoir a tous
il a dit que si G est une partie de F: soit elle est une partie de F :il ya en 2^n possibilité
ou bien elle est partie de FU{a} il y en a egalement 2^n possiblité.
donc le nombre de G est 2^n+2^n=2^(n+1)
mais ce que je n'ai pas compris c'est pourquoi si G est une partie de FU{a} ona 2^n possibilité??? moi je crois plutot que c'est 2^(n+1) possibilite car
Card(FU{a})=n+1.
AIDEZ MOI S'il vous plait
MERCI
Les parties de FU{a} sont de deux sortes : celles qui ne contiennent pas a (et ce sont donc des parties de F) ou celles qui contiennent a et qui sont donc composées de a réuni avec une partie de F.
J'AI CORRIGE TON TEXTE COMME SUIT: DIS MOI SI C'EST MIEUX.
au départ,on a un enemble E à n elements.
si n=1 la relation est verifieé
on l'a suppose vérifiée pour un rang n et on démontre qu'elle est verifiée pour le rang n+1.
donc le prof a considéré un ensemble E de cardinal n+1 et un element a de E.
il a posé E=FU{a} .
donc cardF=n
il a dit que si G est une partie de E: soit elle est une partie de F :il ya en 2^n possibilités.
ou bien c'est une partie de E contenant "a" . il y en a egalement 2^n possiblités car elle est du type {a} U H où H est une partie de quelconque
de F.
donc le nombre de G est 2^n+2^n=2^(n+1)
au départ,on a un enemble E à n elements.
si n=1 la relation est verifieé
on l'a suppose vérifiée pour un rang n et on démontre qu'elle est verifiée pour le rang n+1.
donc le prof a considéré un ensemble E de cardinal n+1 et un element a de E.
il a posé E=FU{a} .
donc cardF=n
il a dit que si G est une partie de E: soit elle est une partie de F :il ya en 2^n possibilités.
ou bien c'est une partie de E contenant "a" . il y en a egalement 2^n possiblités car elle est du type {a} U H où H est une partie de quelconque
de F.
donc le nombre de G est 2^n+2^n=2^(n+1)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
