Pour les intéressés, voici comment j'ai procéder. Solution à débattre éventuellement :
Je note C l'ensemble
)
Considérons les opérateurs
(x)dx)
pour des fonctions h et i continues sur [0,1].
L'idée de cet opérateur est que

.
Le but est alors de montrer qu'il existe une application affine
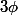
telle que
=0)
.
En fait l'idée est de montrer que plus globalement il existe
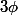
affine telle que

et appliquer alors à

Notons
=ax+b)
. On a alors

S'il existe a et b tels que

vérifie l'énoncé, alors on doit avoir

et vice versa.
Montrons que ce a et b existent.
L'idée est de remarquer que
)
une base du dual de
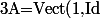)
, espace des fonctions affines (en restreignant l'identité et la fonction 1 à ce dernier bien sûr).
Alors il existe a et b réels tels que

Il ne reste plus qu'à montrer que l'égalité est vraie partout.
Considérons
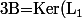\cap Ker(L_{Id_{C}}))
qui n'est autre qu'un supplémentaire de A.
Sur B, l'opérateur

est nul. Pour conclure il nous faut donc montrer que

est nulle sur B.
Soit h dans B (vérifiant donc
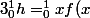dx=0)
) et g la primitive seconde de h vérifiant
=g'(0)=0)
Alors,
=g'(1)-g'(0)=\Bigint_{0}^{1} h=0)
et de même :
=g'(1)-g(1)+g(0)=\Bigint_{0}^{1} xh(x)dx=0)
(IPP)
par conséquent g vérifie les conditions de l'énoncé et on a donc

!
CQFD.
Qu'en pensez-vous?
pour toute fonction g vérifiant les conditions :
pour toute fonction g vérifiant les conditions :