Bonjour, je suis mathématicien amateur.
Je vais rédiger un article sur mon travail.
Les nombres premiers inférieurs à 25 000 sont représentées sur cette image :
Vous avez de plus amples infos sur mon profil linkedin.
C'est tout frais.
Voyez-vous une organisation ?
Bonne soirée
EDIT :
https://erwanallot.com/primal_III/
ps : je ne m'attendais pas à voir ça
Organisation géométrique des nombres premiers
11 messages
- Page 1 sur 1
Re: Organisation géométrique des nombres premiers
Pour la première image, images/primal.png, le résultat obtenu est certainement dû uniquement à la densité des nombres premiers.
Tu peux le vérifier de cette façon.
Tu prends les premiers de 1 à 101 par exemple (tu peux aller un peu plus loin ... l'idée est juste d'éviter les 'problèmes' sur les tout petits nombres). Et tu complètes avec cette formule :
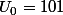
,0))
Tu peux vérifier, cette série donne des nombres 'aléatoires', mais l'ordre de grandeur du k-ème nombre est similaire à l'ordre de grandeur du k-ème nombre premier, même si il faudrait ajouter un petit quelque chose pour coller un peu mieux.
Refais ton dessin avec cette nouvelle série 'aléatoire', et tu vas constater que tu obtiens un dessin très ressemblant.
N'importe quelle série de nombres croissants un peu comparables donnerait ce type de dessin.
Pour les autres dessins, en particulier primal_spi_17000.png, explique mieux comment tu les obtiens.
Tu peux le vérifier de cette façon.
Tu prends les premiers de 1 à 101 par exemple (tu peux aller un peu plus loin ... l'idée est juste d'éviter les 'problèmes' sur les tout petits nombres). Et tu complètes avec cette formule :
Tu peux vérifier, cette série donne des nombres 'aléatoires', mais l'ordre de grandeur du k-ème nombre est similaire à l'ordre de grandeur du k-ème nombre premier, même si il faudrait ajouter un petit quelque chose pour coller un peu mieux.
Refais ton dessin avec cette nouvelle série 'aléatoire', et tu vas constater que tu obtiens un dessin très ressemblant.
N'importe quelle série de nombres croissants un peu comparables donnerait ce type de dessin.
Pour les autres dessins, en particulier primal_spi_17000.png, explique mieux comment tu les obtiens.
Re: Organisation géométrique des nombres premiers
Bonsoir.
Ok, merci beaucoup pour la réponse. Je testerai la comparaison demain.
Ok, merci beaucoup pour la réponse. Je testerai la comparaison demain.
Re: Organisation géométrique des nombres premiers
"Pour les autres dessins, en particulier primal_spi_17000.png, explique mieux comment tu les obtiens."
Ah, j'avais mal lu ta phrase.
Je prends P < 17k, et je réduis la distance entre les pixels tout en les grossissant tous.
Je testerai volontiers ta formule demain pour comparer. Merci.
Je refais différent zoom là et ce sera mieux présenté sur mon site.
On a donc le témoin test N qui est passé. On va faire le témoin test Random.
édit : en fait, ta série, c'est pas du tout random. Mais je la testerai. Merci. C'est noté.
Ah, j'avais mal lu ta phrase.
Je prends P < 17k, et je réduis la distance entre les pixels tout en les grossissant tous.
Je testerai volontiers ta formule demain pour comparer. Merci.
Je refais différent zoom là et ce sera mieux présenté sur mon site.
On a donc le témoin test N qui est passé. On va faire le témoin test Random.
édit : en fait, ta série, c'est pas du tout random. Mais je la testerai. Merci. C'est noté.
Re: Organisation géométrique des nombres premiers
Oui , ma série est 'trop régulière'.
Si tu crées cette série via un tableur, tu peux ajouter/retrancher 1 aléatoirement, avec la fonction rand(), ou alea() en version française. Mais peu importe, c'est uniquement les ordres de grandeur des nombres qui déterminent tout.
Je n'ai pas compris l'explication pour l'image '17K'.
Si tu crées cette série via un tableur, tu peux ajouter/retrancher 1 aléatoirement, avec la fonction rand(), ou alea() en version française. Mais peu importe, c'est uniquement les ordres de grandeur des nombres qui déterminent tout.
Je n'ai pas compris l'explication pour l'image '17K'.
Re: Organisation géométrique des nombres premiers
j'ai pas compris la question
j'ai refait des zooms des images
tu peux retourner sur mon site, y a d'autres images de P
c'est un cycle qui se répète
Pour l'instant, je vois 3 phases.
EDIT :
un œuf,
4 bras
1 carré
5bras
1carré
6bras
1carré
RE_EDIT :
ok, j'ai compris la question ;
en me relisant, je vois que c'est mal indiqué comment je remplis au fur et à mesure la portion d'aire réservée pour un nombre.
Je vais refaire des graphs en décolorant au sein d'un même nombre pour voir dans quel sens je prend les pixels.
Et du coup, je crois vraiment pas que ce soit par hasard que P s'organise. Mais vraiment pas. Et j'en ai trituré des nombres et j'en ai vu des graphs... Là, je sais pas, je trouve ça joli déjà et puis je sais pas... je vais creuser.
...
re_re_edit :
j'ai rajouté une image pour expliquer la sélection du pixel correspondant à P en fonction du "temps primal" et de la "valeur réel" par aire balayée.
j'ai refait des zooms des images
tu peux retourner sur mon site, y a d'autres images de P
c'est un cycle qui se répète
Pour l'instant, je vois 3 phases.
EDIT :
un œuf,
4 bras
1 carré
5bras
1carré
6bras
1carré
RE_EDIT :
ok, j'ai compris la question ;
en me relisant, je vois que c'est mal indiqué comment je remplis au fur et à mesure la portion d'aire réservée pour un nombre.
Je vais refaire des graphs en décolorant au sein d'un même nombre pour voir dans quel sens je prend les pixels.
Et du coup, je crois vraiment pas que ce soit par hasard que P s'organise. Mais vraiment pas. Et j'en ai trituré des nombres et j'en ai vu des graphs... Là, je sais pas, je trouve ça joli déjà et puis je sais pas... je vais creuser.
...
re_re_edit :
j'ai rajouté une image pour expliquer la sélection du pixel correspondant à P en fonction du "temps primal" et de la "valeur réel" par aire balayée.
Re: Organisation géométrique des nombres premiers
Ok, c'est clair pour l'image 17K.
Et du coup, là encore, pas de magie si on obtient cette forme (un carré rempli plus ou moins aléatoirement, puis un cadre avec un trait qui se dessine assez nettement, puis à nouveau un comportement plus ou moins aléatoire).
Je suis totalement convaincu qu'avec les suites ''aléatoires'' que je proposais hier, tu auras un résultat similaire.
C'est juste une question de densité des nombres premiers.
Quand on arrive sur des nombres premiers de l'ordre de 10000 par exemple, on a déjà vu 1200 ou 1300 nombres premiers, la somme de ces nombres premiers donne un nombre de l'ordre de 5 800 000. On a donc déjà rempli un 'losange' de coté 3400 environ. Que le nombre premier suivant soit 10111 ou 10113 ou 10117, ou 10119, ça jouera peu sur l'emplacement de ce pixel, on va 'sauter' 2 diagonales (2x3400=6800), et on va 'avancer' de 3200 pixels environ. Donc on va reculer d'environ 200 pixels. Là, ça va donner un truc pas très marqué.
Mais quand on est proche de 13200, la taille du losange fait qu'on 'avance' de 3 cotés à peu près. Quand est de l'ordre de 13200, la surface du losange est de l'ordre de 9 700 000 , et son coté est de l'ordre de 4400, soit 13200/3. Que le nombre premier suivant soit de 13201 ou 13203 ou 13207, peu importe, seul l'ordre de grandeur est détectable sur ton dessin. J'ai ciblé 13200, parce que dans mes calculs, j'arrive à un coefficient de 2.99927, mais tant qu'on est dans une fourchette entre 2.99 et 3.01, on a un dessin qui est totalement détectable.
Les chiffres que je donne sont approximatifs, je n'ai pas de liste des premiers sous la main pour faire ces calculs, j'utilise la formule que je proposais hier.
Et évidemment, on retrouvera des formes similaires quand la taille du losange fait qu'on 'avance' de 4 cotés etc etc.
Et du coup, là encore, pas de magie si on obtient cette forme (un carré rempli plus ou moins aléatoirement, puis un cadre avec un trait qui se dessine assez nettement, puis à nouveau un comportement plus ou moins aléatoire).
Je suis totalement convaincu qu'avec les suites ''aléatoires'' que je proposais hier, tu auras un résultat similaire.
C'est juste une question de densité des nombres premiers.
Quand on arrive sur des nombres premiers de l'ordre de 10000 par exemple, on a déjà vu 1200 ou 1300 nombres premiers, la somme de ces nombres premiers donne un nombre de l'ordre de 5 800 000. On a donc déjà rempli un 'losange' de coté 3400 environ. Que le nombre premier suivant soit 10111 ou 10113 ou 10117, ou 10119, ça jouera peu sur l'emplacement de ce pixel, on va 'sauter' 2 diagonales (2x3400=6800), et on va 'avancer' de 3200 pixels environ. Donc on va reculer d'environ 200 pixels. Là, ça va donner un truc pas très marqué.
Mais quand on est proche de 13200, la taille du losange fait qu'on 'avance' de 3 cotés à peu près. Quand est de l'ordre de 13200, la surface du losange est de l'ordre de 9 700 000 , et son coté est de l'ordre de 4400, soit 13200/3. Que le nombre premier suivant soit de 13201 ou 13203 ou 13207, peu importe, seul l'ordre de grandeur est détectable sur ton dessin. J'ai ciblé 13200, parce que dans mes calculs, j'arrive à un coefficient de 2.99927, mais tant qu'on est dans une fourchette entre 2.99 et 3.01, on a un dessin qui est totalement détectable.
Les chiffres que je donne sont approximatifs, je n'ai pas de liste des premiers sous la main pour faire ces calculs, j'utilise la formule que je proposais hier.
Et évidemment, on retrouvera des formes similaires quand la taille du losange fait qu'on 'avance' de 4 cotés etc etc.
Re: Organisation géométrique des nombres premiers
Bonjour.
Merci pour ta réponse.
Je n'ai pas tout compris de tes explications, désolé.
J'ai pas compris le "Mais quand on est proche de 13200, la taille du losange fait qu'on 'avance' de 3 cotés à peu près."
En tout cas, oui, je vais tester ta formule pour savoir ce que ça donne.
Je me suis trompé énormément de fois sur les nombres premiers.
(j'ai une autre idée sur de la géométrie atomique que je présenterai ultérieurement)
Donc, pour cette spirale...
1/ comparer avec ta formule
2/ j'ai quand même envie de voir d'autres choses comme la moyenne et des chemins plus une animation
On verra bien.
Donc, oui, commencer par comparer avec ta formule.
Ensuite, je récupère une base de nombres premiers plus grandes pour voir plus loin.
(ensuite, je passe à autre chose)
Merci, je reviendrai pour illustrer ta formule comparé à P.
Bonne journée.
édit :
j'ai fait ta formule. (les images sont sur le site en turquoise)
Ca y ressemble.
Mais y a des différences.
Honnêtement, je sais pas.
Je vais refacto le code pour voir déjà plus loin avec P...
C'était la petite idée depuis 2 ou 3 jours.
Je reviendrai si je trouve des trucs.
Merci.
Bonne journée.
ré édit :
j'ai compris l'histoire d'environ 3 fois la longueur d'un côté
je viens de comprendre
oui, c'est un vrai paramètre... oui, ça explique du coup le truc, ok.
Mais je peux pas m'empêcher de penser que P a quelque chose...
Je reviendrai si je vois un truc sur cette géométrie ou ailleurs.
Merci pour ta réponse.
Je n'ai pas tout compris de tes explications, désolé.
J'ai pas compris le "Mais quand on est proche de 13200, la taille du losange fait qu'on 'avance' de 3 cotés à peu près."
En tout cas, oui, je vais tester ta formule pour savoir ce que ça donne.
Je me suis trompé énormément de fois sur les nombres premiers.
(j'ai une autre idée sur de la géométrie atomique que je présenterai ultérieurement)
Donc, pour cette spirale...
1/ comparer avec ta formule
2/ j'ai quand même envie de voir d'autres choses comme la moyenne et des chemins plus une animation
On verra bien.
Donc, oui, commencer par comparer avec ta formule.
Ensuite, je récupère une base de nombres premiers plus grandes pour voir plus loin.
(ensuite, je passe à autre chose)
Merci, je reviendrai pour illustrer ta formule comparé à P.
Bonne journée.
édit :
j'ai fait ta formule. (les images sont sur le site en turquoise)
Ca y ressemble.
Mais y a des différences.
Honnêtement, je sais pas.
Je vais refacto le code pour voir déjà plus loin avec P...
C'était la petite idée depuis 2 ou 3 jours.
Je reviendrai si je trouve des trucs.
Merci.
Bonne journée.
ré édit :
j'ai compris l'histoire d'environ 3 fois la longueur d'un côté
je viens de comprendre
oui, c'est un vrai paramètre... oui, ça explique du coup le truc, ok.
Mais je peux pas m'empêcher de penser que P a quelque chose...
Je reviendrai si je vois un truc sur cette géométrie ou ailleurs.
Re: Organisation géométrique des nombres premiers
J'ai regardé, et comme prévu, les dessins obtenus sont assez comparables à ceux que tu avais.
Précision, la suite que je propose, c'est :
- commencer par les nombres premiers jusqu'à un certain seuil (101 par exemple) et compléter par une formule du type,0))
A priori, tu a zappé les premiers termes (les nombres premiers jusqu'à 101). Mais l'impact est totalement marginal, il ne touche que le centre du dessin, et avec l'effet de zoom, c'est une partie qui apparaît comme un gros carré rouge quand on traite des grands nombres.
Les nombres premiers sont fascinants, ou plutôt envoutants. Beaucoup de gens font des manipulations sur ces nombres premiers, et tombent sur des résultats qu'ils jugent magiques. Et systématiquement, il n'y a rien de magique dans ces résultats.
Attention, tu as été envouté par ces nombres premiers. Reviens sur terre avant qu'il ne soit trop tard.
J'ai soudain un doute sur les calculs que je faisais ce matin. A un endroit, je multiplie par pour avoir la taille du losange, et je me demande s'il ne fallait pas plutôt diviser par
pour avoir la taille du losange, et je me demande s'il ne fallait pas plutôt diviser par 
Mais dans l'idée, ça ne change rien, ça déplace juste les intervalles où on a des motifs particuliers.
Précision, la suite que je propose, c'est :
- commencer par les nombres premiers jusqu'à un certain seuil (101 par exemple) et compléter par une formule du type
A priori, tu a zappé les premiers termes (les nombres premiers jusqu'à 101). Mais l'impact est totalement marginal, il ne touche que le centre du dessin, et avec l'effet de zoom, c'est une partie qui apparaît comme un gros carré rouge quand on traite des grands nombres.
Les nombres premiers sont fascinants, ou plutôt envoutants. Beaucoup de gens font des manipulations sur ces nombres premiers, et tombent sur des résultats qu'ils jugent magiques. Et systématiquement, il n'y a rien de magique dans ces résultats.
Attention, tu as été envouté par ces nombres premiers. Reviens sur terre avant qu'il ne soit trop tard.
J'ai soudain un doute sur les calculs que je faisais ce matin. A un endroit, je multiplie par
Mais dans l'idée, ça ne change rien, ça déplace juste les intervalles où on a des motifs particuliers.
Re: Organisation géométrique des nombres premiers
Oui, je vais refaire en prenant les P jusqu'à 101.
En comparaison.
Je pourrai aussi les superposer voir...
Oui, ça m'arrive d'être envouté par les nombres premiers.
Disons que quand j'ai des idées, je reviens dessus. C'est un vrai casse-tête. Mais y a des trucs qu'on peut trouver...
J'aimerai me reposer sur de la géométrie.
J'ai une idée que j'ai commencé ici :
https://erwanallot.com/atomique/
L'idée, c'est de créer des figures qui ont la même aire et aussi un centre identique. Donc je dois retravailler ces figures. Je veux visualiser les triangles.
Et si je rajoute le cube de métatron ici :
/Metatron/
Je peux obtenir des tétraèdres ou bien étudier 4 points dans l'espace.
Le tout, c'est déjà de bien harmoniser les 4 éléments.
Donc le projet actuel, c'est juste pour me refaire la main sur le code.
Et l'autre aussi.
J'avais aussi cherché en musique les nombres premiers mais ça casse les oreilles :
/anciensTravauxMaths/musiqueDesNP/
Et autrefois, je m'étais intéressé à un opérateur :
/anciensTravauxMaths/allotion
Ah oui, et pour P, je voulais aussi faire cette spirale mais là, je suis vraiment pas doué pour l'instant en code et là je triture vraiment tout :
/anciensTravauxMaths/spin
Bon, je viens de voir que j'ai détruis l'index de mon site à vouloir éditer sans arrêt mon article/note...
Je sais pas... bon, c'est toujours bien de s'y remettre en tout cas.
Mais oui, les nombres premiers envoutent.
édit :
je reviendrai quand j'aurai refait des choses
et sinon, je trouve quand même que le motif spécial quand il s'agit de P, il a une signature parce qu'il y a une petite bosse... et ça je l'avais déjà remarqué cette bosse en faisant mod(rang*rang;P)
ex pour 2, valeur 2 rang 1 on fait mod(1^2;2)
ré-édit :
j'ai fait la moyenne des coordonnées de chaque quartier
enfin, voilà, je continuerai...
je m'amuse
ré-ré-édit
je viens de faire la moyenne pour ta série 101 en turquoise.
Les bras doublés n'ont pas l'air d'aller dans le même sens sur le long terme.
Mais j'ai pas encore commencé par P jusqu'à 101 pour ta série.
Ou peut-être que si, c'est pareil, faut aller plus loin...
Ouais, ça rebique dans l'autre sens après.
OK.
Bon, je vais bientôt changer de sujet.
Merci beaucoup.
En comparaison.
Je pourrai aussi les superposer voir...
Oui, ça m'arrive d'être envouté par les nombres premiers.
Disons que quand j'ai des idées, je reviens dessus. C'est un vrai casse-tête. Mais y a des trucs qu'on peut trouver...
J'aimerai me reposer sur de la géométrie.
J'ai une idée que j'ai commencé ici :
https://erwanallot.com/atomique/
L'idée, c'est de créer des figures qui ont la même aire et aussi un centre identique. Donc je dois retravailler ces figures. Je veux visualiser les triangles.
Et si je rajoute le cube de métatron ici :
/Metatron/
Je peux obtenir des tétraèdres ou bien étudier 4 points dans l'espace.
Le tout, c'est déjà de bien harmoniser les 4 éléments.
Donc le projet actuel, c'est juste pour me refaire la main sur le code.
Et l'autre aussi.
J'avais aussi cherché en musique les nombres premiers mais ça casse les oreilles :
/anciensTravauxMaths/musiqueDesNP/
Et autrefois, je m'étais intéressé à un opérateur :
/anciensTravauxMaths/allotion
Ah oui, et pour P, je voulais aussi faire cette spirale mais là, je suis vraiment pas doué pour l'instant en code et là je triture vraiment tout :
/anciensTravauxMaths/spin
Bon, je viens de voir que j'ai détruis l'index de mon site à vouloir éditer sans arrêt mon article/note...
Je sais pas... bon, c'est toujours bien de s'y remettre en tout cas.
Mais oui, les nombres premiers envoutent.
édit :
je reviendrai quand j'aurai refait des choses
et sinon, je trouve quand même que le motif spécial quand il s'agit de P, il a une signature parce qu'il y a une petite bosse... et ça je l'avais déjà remarqué cette bosse en faisant mod(rang*rang;P)
ex pour 2, valeur 2 rang 1 on fait mod(1^2;2)
ré-édit :
j'ai fait la moyenne des coordonnées de chaque quartier
enfin, voilà, je continuerai...
je m'amuse
ré-ré-édit
je viens de faire la moyenne pour ta série 101 en turquoise.
Les bras doublés n'ont pas l'air d'aller dans le même sens sur le long terme.
Mais j'ai pas encore commencé par P jusqu'à 101 pour ta série.
Ou peut-être que si, c'est pareil, faut aller plus loin...
Ouais, ça rebique dans l'autre sens après.
OK.
Bon, je vais bientôt changer de sujet.
Merci beaucoup.
Re: Organisation géométrique des nombres premiers
Retour sur ces nombres premiers et sur la spirale d'Ulam (la spirale classique, où on voit des diagonales).
Je t'invite à faire ces 2 expériences.
Dans la spirale d'Ulam, les nombres sont disposés en carrés ( tu as fait aussi des dessins en triangles ou en hexagones, et ça va forcément être intéressant aussi pour ces 2 formes).
Chaque point est colorié en blanc si le nombre correspondant est composé, et en noir si ce nombre est premier.
Expérience 1 : modifie la règle, en dessinant un point noir si le nombre n'est multiple ni de 2, ni de 3, ni de 5. Et un point blanc pour tout nombre multiple de 2, 3 ou 5.
Tu vas obtenir une forme assez ressemblante à la spirale d'Ulam. Les diagonales qu'on peut voir dans la spirale d'Ulam sont totalement là. Elles sont en traits continus, alors que dans la vraie spirale, elles sont en pointillé.
A priori, on a un motif de taille 30x30 qui se répète régulièrement (sur la partie droite, un autre motif 30x30 sur la partie basse etc)
Expérience 2 : Les nombres premiers sont évidemment parmi ceux qui ne sont pas multiples de 2, de 3 ou de 5 (sauf 2,3 et 5 eux-mêmes) donc parmi les points noirs du 1er dessin.
Et pour des nombres de l'ordre de 2000 ou 5000, il y a une grosse moitié de ces nombres qui sont premiers.
Du coup, pour tous les nombres non multiples de 2 ni de 3 ni de 5, tu peux dessiner un point soit noir soit blanc (avec une fonction aléatoire par exemple), pour reproduire l'effet 'pointillé'.
Et le dessin obtenu sera très ressemblant à la vraie spirale d'Ulam.
Je t'invite à faire ces 2 expériences.
Dans la spirale d'Ulam, les nombres sont disposés en carrés ( tu as fait aussi des dessins en triangles ou en hexagones, et ça va forcément être intéressant aussi pour ces 2 formes).
Chaque point est colorié en blanc si le nombre correspondant est composé, et en noir si ce nombre est premier.
Expérience 1 : modifie la règle, en dessinant un point noir si le nombre n'est multiple ni de 2, ni de 3, ni de 5. Et un point blanc pour tout nombre multiple de 2, 3 ou 5.
Tu vas obtenir une forme assez ressemblante à la spirale d'Ulam. Les diagonales qu'on peut voir dans la spirale d'Ulam sont totalement là. Elles sont en traits continus, alors que dans la vraie spirale, elles sont en pointillé.
A priori, on a un motif de taille 30x30 qui se répète régulièrement (sur la partie droite, un autre motif 30x30 sur la partie basse etc)
Expérience 2 : Les nombres premiers sont évidemment parmi ceux qui ne sont pas multiples de 2, de 3 ou de 5 (sauf 2,3 et 5 eux-mêmes) donc parmi les points noirs du 1er dessin.
Et pour des nombres de l'ordre de 2000 ou 5000, il y a une grosse moitié de ces nombres qui sont premiers.
Du coup, pour tous les nombres non multiples de 2 ni de 3 ni de 5, tu peux dessiner un point soit noir soit blanc (avec une fonction aléatoire par exemple), pour reproduire l'effet 'pointillé'.
Et le dessin obtenu sera très ressemblant à la vraie spirale d'Ulam.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
