Ordre de 2 modulo p dans un exercice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par JasonMendoza » 26 Fév 2022, 14:17
par JasonMendoza » 26 Fév 2022, 14:17
Bonjour,
Je suis en train de faire l'exercice suivant :

Et la correction est la suivante :

Je comprends tout jusqu'à "Dès lors,

divise p-1 et 2(q-1)
mais ne divise pas q-1." Pourquoi ne divise-t-il pas q-1? A priori il se pourrait que

non?
Merci d'avance!
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Fév 2022, 14:36
par GaBuZoMeu » 26 Fév 2022, 14:36
Bonjour,
Combien vaut

modulo

?
 par JasonMendoza » 26 Fév 2022, 14:58
par JasonMendoza » 26 Fév 2022, 14:58
Ah cela vaut 1?
Car p divise

?
Merci!!
Mais du coup, à propos de la partie "il se pourrait que

". Comment cela se fait-il qu'il divise p-1 et pas q-1?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Fév 2022, 20:21
par GaBuZoMeu » 26 Fév 2022, 20:21
Non, ça vaut

. Et donc l'ordre de 2 modulo

ne divise pas
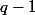
.
 par JasonMendoza » 26 Fév 2022, 21:09
par JasonMendoza » 26 Fév 2022, 21:09
Ah oui pardon, une étourderie de ma part ...
Pour ma deuxième question, j'ai un peu réfléchi, et comme on raisonne par l'absurde, on peut en fait déjà éliminer tous les cas p = q (même si pas nécessaire) puisque si p=q y a contradition et dans le reste des cas à la fin de la preuve on trouve aussi une contradiction. Est-ce un raisonnement valable mathématiquement?
Merci!!
 par JasonMendoza » 28 Fév 2022, 16:02
par JasonMendoza » 28 Fév 2022, 16:02
GaBuZoMeu a écrit:Non, ça vaut

. Et donc l'ordre de 2 modulo

ne divise pas
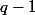
.
Je reviens vers vous car un truc m'échappe, dans notre cours on a cette implication:

Mais là on utilise l'autre sens de cette implication (plus précisément la contraposée de l'autre implication). Est-ce donc une équivalence?
EDIT : en fait ça se démontre bien puisque la congruence est compatible avec la mise à la puissance et que

. Mais comment ça se fait qu'on n'est pas écrit une équivalence dans notre cours alors??
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 28 Fév 2022, 17:18
par GaBuZoMeu » 28 Fév 2022, 17:18
Peut-*etre parce qu'on a pensé que ça tombait sous le sens ?
Cela va sans dire, mais cela va mieux en le disant.

 par JasonMendoza » 28 Fév 2022, 18:15
par JasonMendoza » 28 Fév 2022, 18:15
Ok! J'aurai trouvé ça plus clair qu'on dise que ce soit une équivalence si c'en est une, même si l'un des côtés est trivial, mais comme j'ai trouvé la démonstration presque immédiatement, je comprends pourquoi on peut considérer que cela tombe sous sens.
Merci pour l'aide!!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités




. Et donc l'ordre de 2 modulo
ne divise pas
.
