Ordre d'un Groupe

[Xavier63]

J'ai une question de débutant

soit le groupe G = ((Z/3Z)², +)

je ne comprends pas pourquoi il est d'ordre 1 ou 3

nous avons (Z/3Z, +) = {0, 1, 2 }

donc pour moi G est d'ordre 9, c'est à dire toute les combinaisons {0, 1, 2 } x {0, 1, 2 }

Question supplémentaire, quel est l'ordre du groupe H = (Z/2Z, +) x (Z/4Z, +) ?

[GaBuZoMeu]

Tu dois confondre : on ne te dit sûrement pas que ce groupe est d'ordre 3, mais que tout élément dedans est d'ordre 3 (ou 1 pour l'identité).

[Xavier63]

Enfin la question demandé, c'est de dire si le groupe G = ((Z/3Z)², +) et H= (Z/9Z, +) sont isomorphe, la réponse est négative, sans démonstration. En effet il est dit que les éléments de G sont d'ordre 3 et 1. D'ordre 3 je suis d'accord mais d'ordre un je ne vois pas

[Xavier63]

oui l'élement 0 est d'ordre 1

[Xavier63]

Je ne vois pas pourquoi les groupe G = ((Z/3Z)², +) et H= (Z/9Z, +) ne sont pas isomorphes


Question supplémentaire, quel est l'ordre du groupe H = (Z/2Z, +) x (Z/4Z, +) ?

[GaBuZoMeu]

Quel est l'ordre de 1 dans (Z/9Z,+) ?

[Xavier63]

1 a un ordre de 9 dans (Z/9Z,+)

Je devine que la question suivante est l'ordre de 1 dans (Z/3Z)² et je présume que c'est 3, pourtant je penserais que c'est 9

De même que l'ordre du groupe H = (Z/2Z, +) x (Z/4Z, +) est 4

Par contre si j'avais H = (Z/2Z, +) x (Z/3Z, +) cette fois 1 est d'ordre 6 { (1,1), (0,2), (1,0), (0,1), (1,2), (0,0)}

???

[GaBuZoMeu]

Tu es perdu, là.
Un conseil, passe une bonne nuit. Demain matin tu seras sans doute en état de faire la différence entre l'ordre d'un groupe et l'ordre d'un élément dans un groupe.
Et tu verras que "1 dans (Z/3Z)²" n'a pas de sens : les éléments de (Z/3Z)² sont des couples d'entiers modulo 3.

Bonne nuit !

[tournesol]

de même que l'ordre de H=(Z/2Z ,+)X(Z/4Z,+) est 4 ?
As tu compris que l'ordre d'un groupe , c'est son cardinal ?
Le cardinal du produit de deux ensembles finis A et B est égal à (card A)×(card B)
Donc H est d'ordre 8 .
L'ordre d'un élément est par définition l'ordre du sous groupe qu'il engendre , c'est à dire le cardinal du sous groupe qu'il engendre .
Pour résoudre ton pb , il te reste à démontrer que l'image d'un élément d'ordre d par un isomorphisme de groupes est lui aussi d'ordre d .

[Xavier63]

Pour H = (Z/9Z, +) est un groupe d'ordre 9, H = {0, 1, 2, 3, 4, 5, 6, 7, 8}
l'élément 0 est d'ordre 1
l'élément 1 d'ordre 9
l'élément 2 d'ordre 9 car 2 est premier avec 9
l'élément 3 d'ordre 3
l'élément 4 d'ordre 9 car 4 est premier avec 9
l'élément 5 d'ordre 9 car 5 est premier avec 9
l'élément 6 d'ordre 3
l'élément 7 d'ordre 9 car 7 est premier avec 9
l'élément 8 d'ordre 9 car 8 est premier avec 9

La question étant, de démontrer que H = (Z/9Z, +) et G =((Z/3Z)², +) ne sont pas isomorphe

Si j'ai bien compris G =((Z/3Z)², +) est d'ordre 9 et les éléments de G sont toutes les combinaisons {0, 1, 2 } x {0, 1, 2 } càd: {(0,0), (0,1), (1, 0), (1, 1), (1, 2), (2, 1), (2,2), (0,2), (2,0)} et l'ordre de chacun de ses éléments ? Je ne sais pas faire pour un couple ! enfin je pense que c'est

(0,0) est d'ordre 1
(0,1) engendre les sous groupe {(0, 0), (0, 1), (0, 2)}
(1,0) engendre les sous groupe {(0, 0), (1, 0), (2, 0)}
(1,1) engendre les sous groupe {(0, 0), (1, 1), (2, 2)}
(2,0) engendre les sous groupe {(0, 0), (2, 0), (1, 0)}
(0,2) engendre les sous groupe {(0, 0), (0, 2), (0, 1)}
(1,2) engendre les sous groupe {(0, 0), (1, 2), (2, 1)}
(2,1) engendre les sous groupe {(0, 0), (2, 1), (1, 2)}
(2,0) engendre les sous groupe {(0, 0), (2, 0), (1, 0)}
(2,2) engendre les sous groupe {(0, 0), (2, 2), (1, 1)}

Donc les éléments sont d'ordre 1 ou 3
H = (Z/9Z, +) et G =((Z/3Z)², +) ne sont pas isomorphes car on ne peut pas faire de bijection entre les sous groupes engendrés par les éléments de H et les sous groupes engendrés par les éléments de G

Est-ce juste?

[Xavier63]

De même les groupes G = (Z/8Z, +) et H = (Z/2Z, +) x (Z/4Z, +) ne sont pas isomorphe

G = (Z/8Z, +) = {0, 1, 2, 3, 4, 5, 6, 7}
l'élément 0 est d'ordre 1
l'élément 1 d'ordre 8
l'élément 2 d'ordre 4
l'élément 3 d'ordre 8 car 3 est premier avec 8
l'élément 4 d'ordre 2
l'élément 5 d'ordre 8 car 5 est premier avec 8
l'élément 6 d'ordre 4
l'élément 7 d'ordre 8 car 7 est premier avec 8

H = (Z/2Z, +) x (Z/4Z, +) est d'ordre 8 et les éléments de H sont toutes les combinaisons {0, 1, } x {0, 1, 2,3 } càd: {(0,0), (0,1), (1, 0), (1, 1), (1, 2), (1, 3), (0,2), (0,3)} et l'ordre de chacun de ses éléments ?

(0,0) est d'ordre 1
(0,1) engendre les sous groupe {(0, 0), (0, 1), (0, 2), (0, 3)}
(1,0) engendre les sous groupe {(0, 0), (1, 0)}
(1,1) engendre les sous groupe {(0, 0), (1, 1), (0, 2), (1, 3)}
(1,2) engendre les sous groupe {(0, 0), (1, 2)}
(1,3) engendre les sous groupe {(0, 0), (1, 3), (0, 2),(1, 1)}
(0,2) engendre les sous groupe {(0, 0), (0, 2)}
(0,3) engendre les sous groupe {(0, 0), (0, 3), (0, 2), (0, 1)}
(1,3) engendre les sous groupe {(0, 0), (1, 3), (0, 2), (1, 1)}

Donc les éléments sont d'ordre 1, 2 ou 4
G = (Z/8Z, +) et H = (Z/2Z, +) x (Z/4Z, +) ne sont pas isomorphes car on ne peut pas faire de bijection entre les sous groupes engendrés par les éléments de H et les sous groupes engendrés par les éléments de G

[Xavier63]

pardon pour la faute de frappe "les" à la place de "le" : (0,1) engendre le sous groupe ...

[tournesol]

Tu as tres bien compris ce qu'est l'ordre d'un élément .
Avec une bijection , c'est peut être possible mais un isomorphisme est bien plus qu'une bijection.
Dans Z/9Z , il y a 1 sg d'ordre 1 , 1 sg d'ordre 3 , et 1 sg d'ordre 9 .
Dans (Z/3Z)^2 , il y a 1 sg d'ordre 1 , 4 sg d'ordre 3 et 1 sg d'ordre 9 .
Donc isomorphisme ou pas , il ne peut pas exister de bijection entre les sg de G et ceux de H car dans la réunion des 4 sg d'ordre 3 de G , il y a au moins 4 éléments (en fait 9 ) alors qu'il n'y en a que 3 dans le seul sg d'ordre 3 de H . C'est donc un bon argument à condition d'argumenter comme je l'ai fait .
Mais il aurait pu y avoir la même composition en sous groupe .
Par contre dans H il y a des éléments d'ordre 9 et l'image d'un tel élément par un isomorphisme de groupe est un elément d'ordre 9 . Or il n'y en a pas dans G . D'ou l'absence d'isomorphisme .

[tournesol]

Plus géneralement , si deux groupes sont isomorphes alors ils ont pour tout entier n le meme nombre d'eléments d'ordre n , ce nombre pouvant être nul .On peut resumer celà avec un indicateur qui est une partie de NXN.
Abscisse: le nombre d'éléments , Ordonée l'ordre .
Pour Z/9/Z:{(1;1),(2;3),(6;9)}
Pour (Z/3Z)^2 : {(1;1),(8;3)}
Donc pas les mêmes indicateurs , pas isomorphe .
Pour Z/8Z:{(1;1),(1;2),(2;4),(4;8)}
Pour (Z/2Z)X(Z/4Z):{(1;1),(1;2),(6;4)}
Pas isomorphes .

[Xavier63]

En considérant tes critères je trouve une réponse une réponse différente pour (Z/2Z)X(Z/4Z)

Pour Z/8Z:{(1;1),(1;2),(2;4),(4;8)}
Pour (Z/2Z)X(Z/4Z):{(1;1),(3;2),(4;4)} et non {(+;1),(1;2),(6;4)}

en effet
H = (Z/2Z, +) x (Z/4Z, +)

(0,0) est d'ordre 1
(0,1) engendre les sous groupe {(0, 0), (0, 1), (0, 2), (0, 3)}
(1,0) engendre les sous groupe {(0, 0), (1, 0)}
(1,1) engendre les sous groupe {(0, 0), (1, 1), (0, 2), (1, 3)}
(1,2) engendre les sous groupe {(0, 0), (1, 2)}
(1,3) engendre les sous groupe {(0, 0), (1, 3), (0, 2),(1, 1)}
(0,2) engendre les sous groupe {(0, 0), (0, 2)}
(0,3) engendre les sous groupe {(0, 0), (0, 3), (0, 2), (0, 1)}

rassure moi que j'ai bien compris !

[tournesol]

Oui , je te rassure . J'ai été étourdi .

[tournesol]

L'ordre d'un élément est invariant par isomorphisme .
Donc: isomorphisme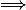 même indicateur . E t la contraposée est pratique .
Mais je ne garantis pas la réciproque .
AU SECOURS LES COLLEGUES ??????

[Xavier63]

Pour les groupes U(Z/7Z) et U(Z/9Z)

Le groupe U(Z/9Z) = {1,2,4,5,7,8} est un groupe cyclique d'ordre 6.
Il possède 4 sous groupes : {1}, {1,8}, {1,4,7}, {1,2,4,5,7,8} d'ordres 1, 2, 3 et 6

U(Z/7Z) = (Z/7Z, +) - {0}
Le groupe U(Z/7Z) = {1,2,4,5,6,7} est un groupe cyclique d'ordre 6.
Il possède 4 sous groupes : {1}, {1,6}, {1,2,4}, {1,2,4,5,6,7} d'ordres 1, 2, 3 et 6

Pour U(Z/9Z):{(1;1),(1;2),(2;3),(2;6)}
Pour U(Z/7Z):{(1;1),(1;2),(2;3), (2, 6)}

donc U(Z/7Z) et U(Z/9Z) sont isomorphes

[GaBuZoMeu]

Xavier63, ton argument pour l'isomorphie des groupes multiplicatifs dans Z/9Z et dans Z/7Z ne tient pas (voir plus bas). Par contre il y a un argument beaucoup plus simple : deux groupes cycliques de même ordre sont isomorphes (je te laisse le démontrer en utilisant des générateurs pour chacun des groupes.

Deux groupes finis peuvent avoir le même nombre d'éléments de chaque ordre sans être isomorphes. Je crois que le plus petit exemple est donné par le groupe de Pauli et le groupe Z/4Z x (Z/2Z)². Ce sont deux groupes d'ordre 16 qui ont un élément d'ordre 1, sept d'ordre 2 et 8 d'ordre 4. Le premier est non commutatif, le deuxième est commutatif. Je pense que c'est le plus petit exemple, mais je n'en suis pas sûr.
Il ne suffit donc pas de considérer l'ordre des éléments pour établir l'isomorphie de deux groupes.

[tournesol]

Ton DONC ne conviens pas . Je t'ai dit que je ne garantissais pas la réciproque ie : même indic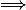isomorphes .
Dans ton cas très interressant , tes deux groupes sont isomorphes car tous les groupes cycliques d'ordre n sont isomorphes à Z/nZ .
Je pense que la réciproque est exacte pour les groupes commutatifs car leur structure est connue : ils sont produits de groupes cycliques d'une certaine façon . Mais j'attend la confirmation de mes collègues .